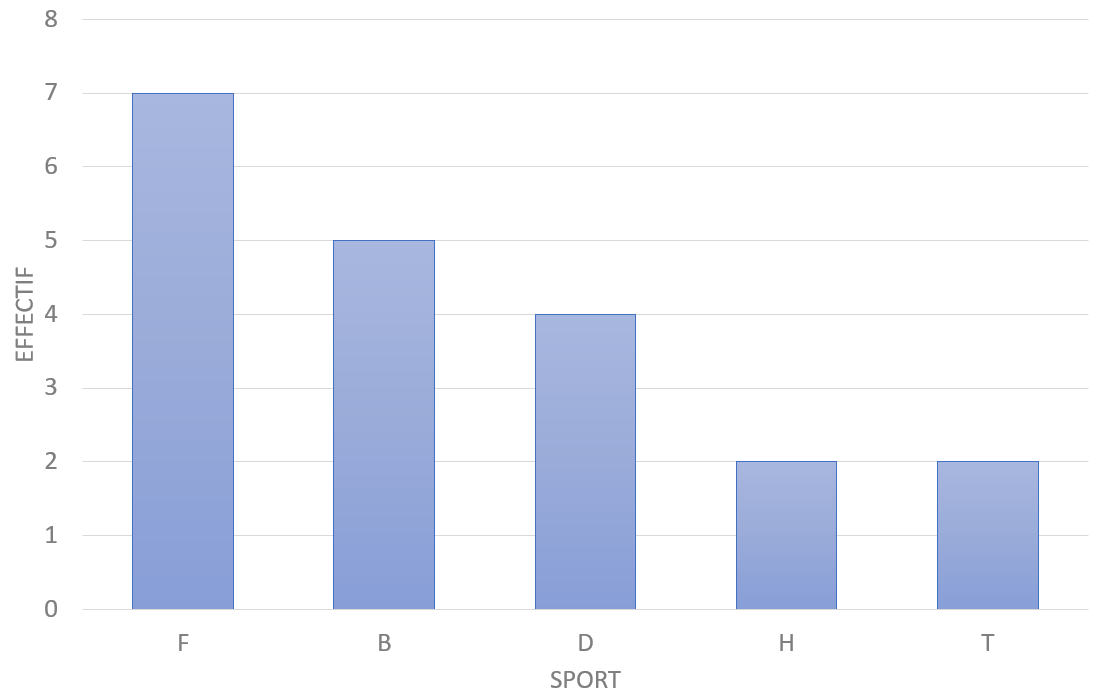AP1 - Statistiques
I – Séries statistiques
Lors d'une étude statistique, on étudie sur une population un caractère qui peut prendre plusieurs valeurs.
On a interrogé 20 élèves de 5ème sur leur sport préféré. Voici leurs réponses :
F - B - D - H - F - D - B - H - F - F - B - T - D - D - F - B - F - T - F - B
Légende : F : Football - B : Basket - D : Danse - H : Handball - T : Tennis
Dans cette enquête, la population étudiée est celle des élèves d'une classe.
Le caractère étudié est le sport préféré des élèves.
Les valeurs possibles du caractère sont : Football, Basket, Danse, Handball et Tennis.
II – Fréquence – pourcentage
La fréquence d'une valeur est le quotient :
| Effectif de la valeur |
| Effectif total |
Elle peut être exprimée sous forme décimale (exacte ou approchée) ou fractionnaire.
C'est un nombre entre 0 et 1.
Plus la fréquence est grande, plus la valeur est fréquente…
La somme des fréquences doit être égale à 1
La fréquence en pourcentage est l'écriture de la fréquence sous forme de pourcentage :
| Effectif de la valeur |
| Effectif total |
× 100
La somme des fréquences en pourcentage doit être égale à 100%
Avec les données précédentes
| Sport |
F |
B |
D |
H |
T |
Total |
| Effectif |
7 |
5 |
4 |
2 |
2 |
20 |
| Fréquence |
|
|
|
|
|
= 1 |
| Fréquence en % |
35% |
25% |
20% |
10% |
10% |
100% |
III – Représentations graphiques
1 – Diagramme en barres
Dans un diagramme en barres, la hauteur de chaque barre est proportionnelle à l'effectif ou à la fréquence qu'elle représente
Avec les données précédentes
| Sport |
F |
B |
D |
H |
T |
Total |
| Effectif |
7 |
5 |
4 |
2 |
2 |
20 |
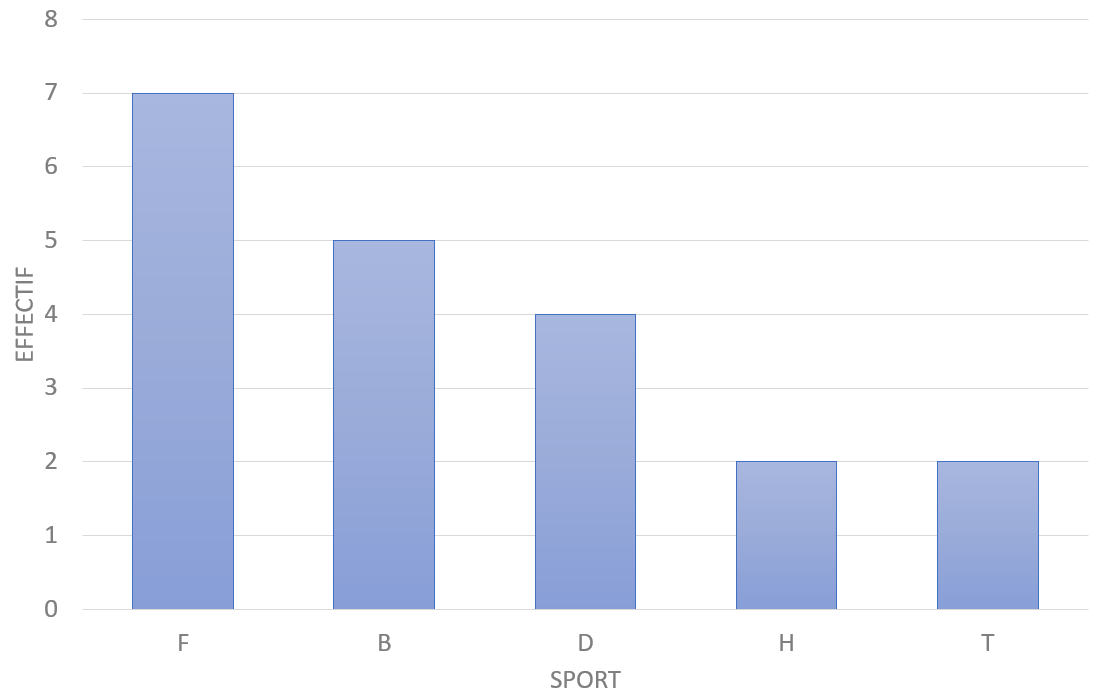
Il n'y a pas d'échelle sur l'axe horizontale mais le nom de chaque barre (ce qu'elle représente).
2 – Diagramme circulaire
Dans un diagramme circulaire, l'angle de chaque secteur est proportionnelle à l'effectif ou à la fréquence qu'elle représente
Avec les données précédentes
| Note |
F |
B |
D |
H |
T |
Total |
| Effectif |
7 |
5 |
4 |
2 |
2 |
20 |
| Angle en ° |
126 |
90 |
72 |
36 |
36 |
360 |

IV – Une caractéristique de position : la moyenne
On va utiliser les données suivantes qui sont des rélevés de notes de trois élèves.
Voici les dernières notes qu’ont obtenues 3 élèves :
Jérôme : 4 ; 6 ; 18 ; 7 ; 17 ; 12 ; 12 ; 18
Bertrand : 13 ; 13 ; 12 ; 10 ; 12 ; 3 ; 14 ; 12 ; 14 ; 15
Yennefer : 15 ; 9 ; 14 ; 13 ; 10 ; 12 ; 12 ; 11 ; 10
Moyenne = | Somme des valeurs |
| Effectif total |
MoyenneJérôme = (4 + 6 + 18 + 7 + 17 + 12 + 12 + 18) ÷ 8 = ......... ≈ ..........
MoyenneBertrand = (13+13+12+10+12+3+14+12+14+15) ÷ 10 = .......
MoyenneYennefer = (15 + 9 +14 + 13 + 10 + 12 + 12 + 11 + 10) ÷ 9 ≈ .......
La moyenne est une caractéristique de position.
On peut gagner du temps avec une moyenne pondérée ou moyenne avec coefficients.
Par exemple pour Bertrand il suffit de créer le tableau suivant :
| Note |
3 |
10 |
12 |
13 |
14 |
15 |
Total |
| Effectif |
1 |
1 |
3 |
2 |
2 |
1 |
10 |
L’effectif de la note 12 est le nombre de fois qu’elle apparait dans la série des notes de Bertrand.
MoyenneBertrand = (1×3 + 1×10 + 3×12 + 2×13 + 2×14 + 1×15) ÷ 10