AP2 - Probabilités

I - Vocabulaire

Une expérience aléatoire est une expérience dont on connait toutes les issues mais dont on ne peut prédire le résultat.

On lance un dé à 6 faces et on observe la face obtenue.

Les issues d'une expérience aléatoire sont appelées les événements élémentaires.

Les 6 événements élémentaires de l'expérience précédente sont « Obtenir 1 », « Obtenir 2 », « Obtenir 3 », « Obtenir 4 », « Obtenir 5 » et « Obtenir 6 ».

Pour une expérience aléatoire, nous allons étudier des événements.

Avec la même expérience :
A=« Obtenir une face paire » qui est satisfait par les 3 événements élémentaires « Obtenir 2 », « Obtenir 4 » et « Obtenir 6 »
B=« Obtenir une face multiple de 3 » qui est satisfait par les 2 événements élémentaires « Obtenir 3 » et « Obtenir 6 »
C=« Ne pas obtenir 4 » qui est satisfait par les 5 événements élémentaires « Obtenir 1 », « Obtenir 2 », « Obtenir 3 », « Obtenir 5 » et « Obtenir 6 »
D=« Obtenir moins de 7 » qui est satisfait par tous les événements élémentaires. On dit que cet événement est certain.
E=« Obtenir plus de 7 » qui n'est satisfait par aucun événement élémentaire. On dit que cet événement est impossible.

Pour une expérience aléatoire, la probabilité d'un événement A est noté P(A) et on a P(A)=
Nombre d'issues favorables à A
Nombre total d'issues

Avec les événements précédents :
P(A)=
3
6

P(B)=
2
6

P(C)=
5
6

P(D)=
6
6
= 1
P(E)=
0
6
= 0

La probabilité d'un événement est un nombre compris entre 0 et 1

La probabilité d'un événement certain est égale à 1. La probabilité d'un événement impossible est égale à 0.

II - Tirages simultanés

On va s'intéresser dans ce paragraphe aux expériences où on fait simultanément deux lancés.

On lance simultanément deux dés à six faces et on effectue la somme des faces obtenues.
Calculer la probabimité des événements suivants :
A=« Obtenir 4 »
B=« Obtenir 9 ou plus »
C=« Obtenir un multipe de 3 »

on va créer un tableau à double entrée (1 pour chaque dé ici) où on va écrire toutes les issues possibles (les somme des faces ici)

+Dé 1
123456
Dé 212►3►45►67
2►3►45►678
3►45►678►►9
45►678►►9►10
5►678►9►►10►11
678►►9►10►11►►12
On remarque que le nombre total d'issues est égal à 6 × 6 =36. Il ne reste plus qu'à compter les issues favorables à chaque événement.
P(A)=
3
36

P(B)=
10
36

P(C)=
12
36

III - Tirages successifs ...

On va s'intéresser dans ce paragraphe aux expériences où on fait sucessivement des lancés. L'expérience type est la suivante :
Dans un sac, il y a des boules indicernables au touché mais de couleur différente. On tire successivement des boules et on étudie la probabilité de certaines combinaisons.

on va créer un arbre de probabilité qui va décrire l'expérience.

1 - Arbre de probabilité

Voici un arbre de probabilité :
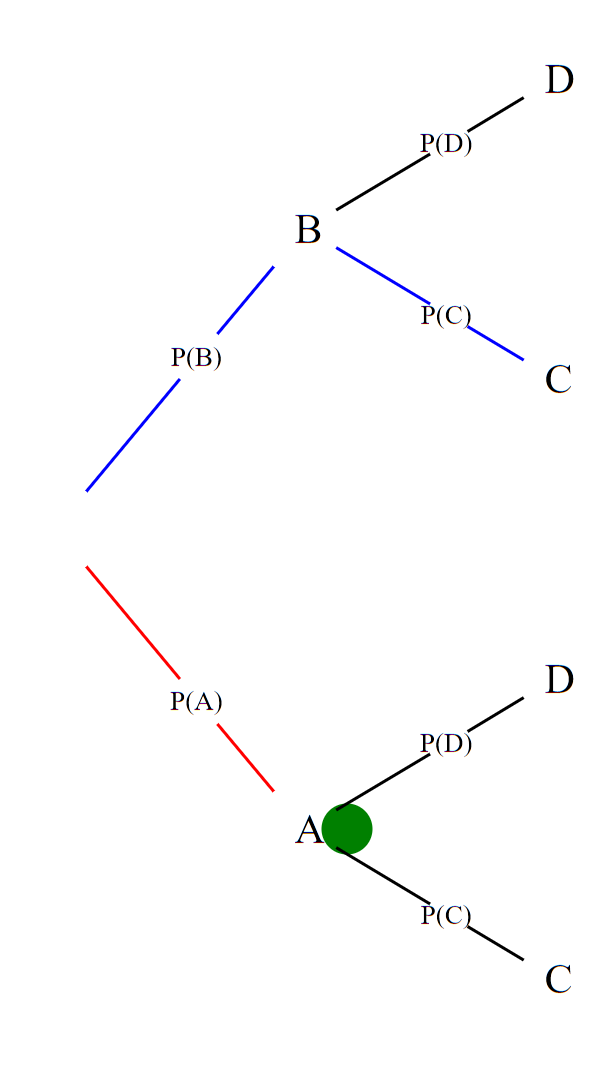─── une branche
─── un chemin
   ●    un noeud

Pour effectuer des calculs à l'aide e cet arbre, on va utiliser les 3 théorèmes suivants :

La somme des probabilités des branches issues d'un même noeud doit être égale à 1.

La probabilité d'un chemin est égale au produit des probabilités des branches qui le composent.

La probabilité d'un événement est égal à la sommme des probabilités des chemins qui le satisfont.

2 - ... avec remise

Dans un sac, il y a 9 boules indicernables au touché mais de couleur différente.
- 5 boules rouges
- 3 boules vertes
- 1 boules noire
On tire successivement deux boules avec remise et on regarde la combinaison obtenue. Calculer les probabilités des événements suivants :
A = « Obtenir au moins une boule rouge »
B = « Obtenir une boule verte puis une noire »
C = « Obtenir une boule verte et une noire »
D = « Obtenir une boule verte ou une noire »



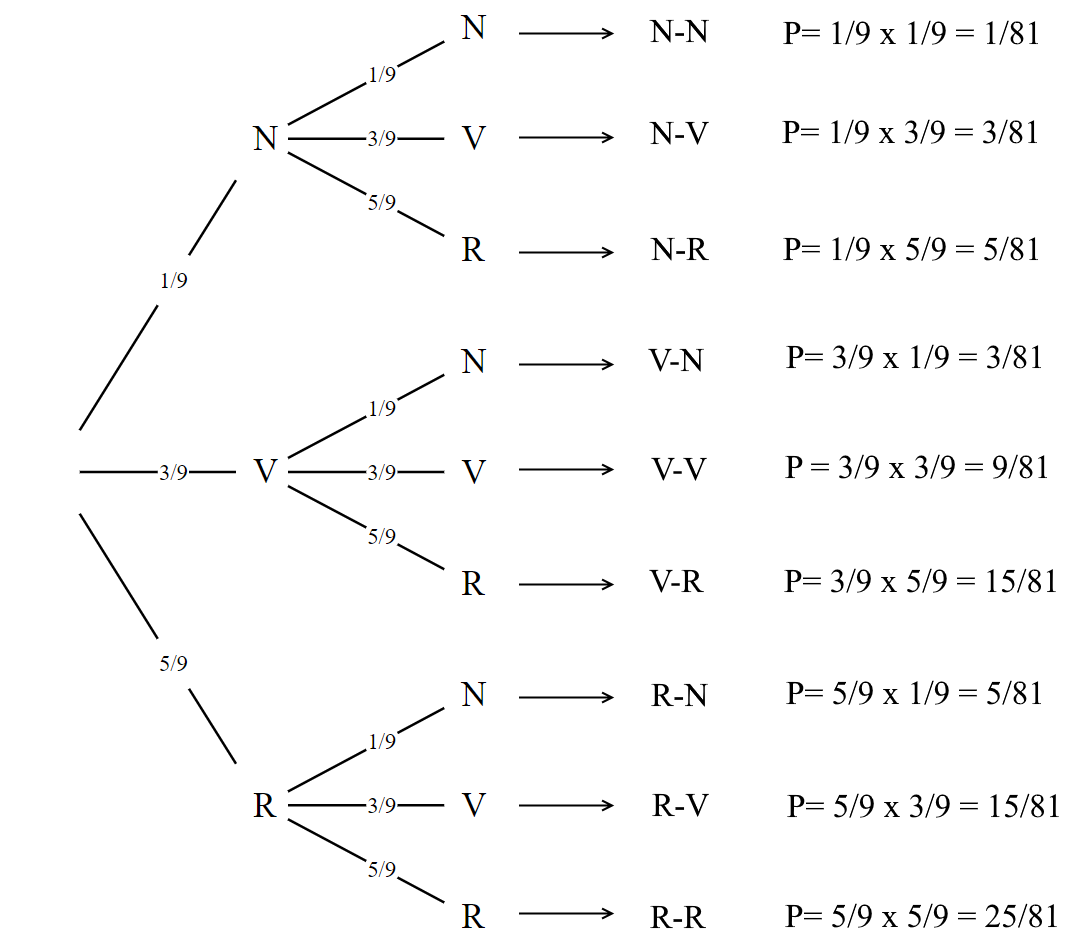
Il ne reste plus qu'à calculer les probabilités.
P(A)=P(«RR»)+P(«RV»)+P(«RN»)+P(«VR»)+P(«NR») =
25
81
+
15
81
+
5
81
+
15
81
+
5
81
=
65
81

P(B)=P(«VN») =
3
81

P(C)=P(«VN»)+P(«NV») =
3
81
+
3
81
=
6
81


P(D)=P(«NN»)+P(«NV»)+P(«NR»)+P(«VN»)+P(«VV»)+P(«VR»)+P(«RN»)+P(«RV»)
        =
1
81
+
3
81
+
5
81
+
3
81
+
9
81
+
15
81
+
5
81
+
15
81
=
56
81

3 - ... sans remise

Dans un sac, il y a 9 boules indicernables au touché mais de couleur différente.
- 5 boules rouges
- 3 boules vertes
- 1 boules noire
On tire successivement deux boules sans remise et on regarde la combinaison obtenue. Calculer les probabilités des événements suivants :
A = « Obtenir au moins une boule rouge »
B = « Obtenir une boule verte puis une noire »
C = « Obtenir une boule verte et une noire »
D = « Obtenir une boule verte ou une noire »



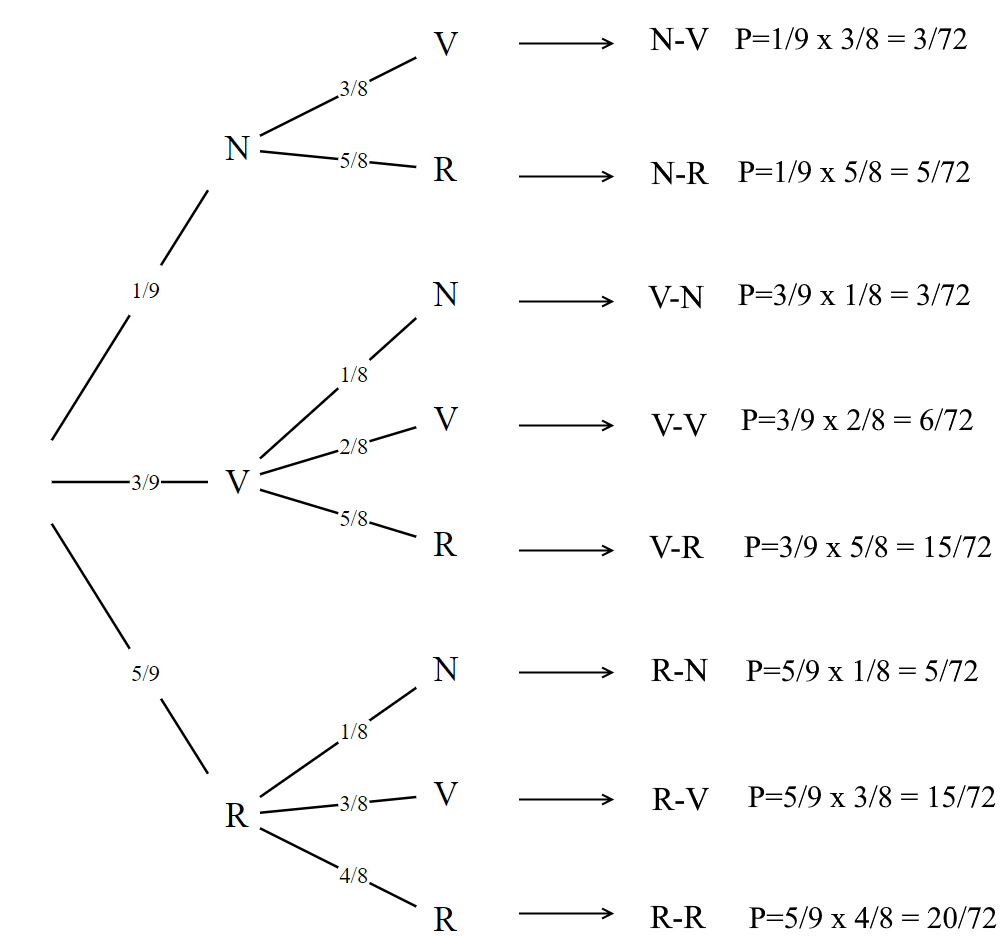
Il ne reste plus qu'à calculer les probabilités.
P(A)=P(«RR»)+P(«RV»)+P(«RN»)+P(«VR»)+P(«NR») =
20
72
+
15
72
+
5
72
+
15
72
+
5
72
=
60
72

P(B)=P(«VN») =
3
72

P(C)=P(«VN»)+P(«NV») =
3
72
+
3
72
=
6
72


P(D)=P(«NV»)+P(«NR»)+P(«VN»)+P(«VV»)+P(«VR»)+P(«RN»)+P(«RV»)
        =
3
72
+
5
72
+
3
72
+
6
72
+
15
72
+
5
72
+
15
72
=
52
72

IV - Fréquence et probabilité

On considère l'expérience suivante :
On lance une pièce équilibrée et on regarde la face obtenue.
La probabilité d'obtenir «Pile» est
1
2
.
On va maintenant utiliser cette expérience pour faire des statistiques :
On va regarder la fréquence de sortie de la face pile en fonction du nombre de lancés.
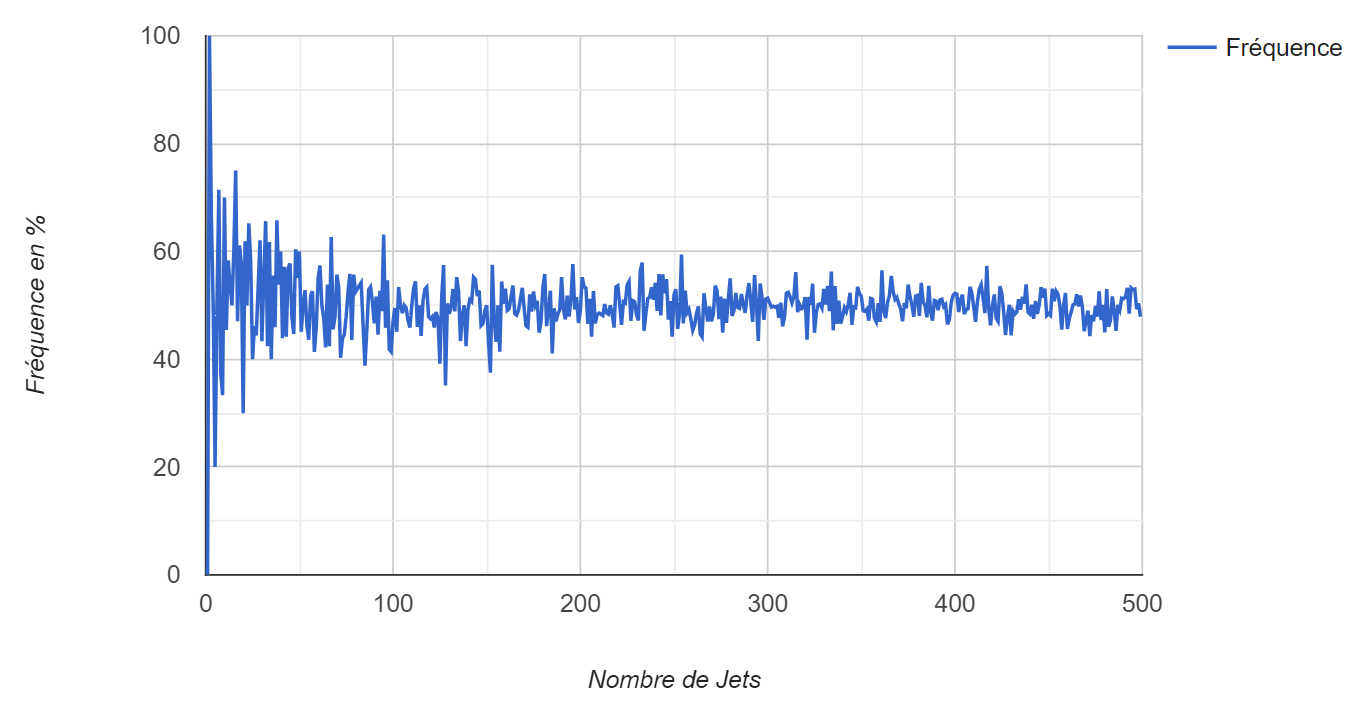
On s'aperçoit que la fréquence se stabilise vers une valeur égale à 0,5.

Quand l'effectif total augmente, la fréquence d'un événement tend vers la probabilité de cet événement