G1 - Théorème de Thalès

0 - Propriété de Pythagore

On utilise la propriété de Pythagore quand on a un triangle rectangle, qu’on connaît les longueurs de 2 côtés et qu’on veut calculer celle du troisième.

Soit PEC un triangle rectangle en E tel que EP=8cm et EC=5cm. Déterminer au millimètre près la longueur du côté [CP].
Solution :
Faire une figure à main levée et y inscrire ce qu’on connaît.

On cherche l’hypoténuse et on connaît les côtés de l’angle droit dans un triangle rectangle.
Le triangle PEC est rectangle en E, d’après la propriété de Pythagore on a :
PC2 = EP2 + EC2
PC2 = 82 + 52
PC2 = 64 + 25
PC2 = 89
PC = √89
PC ≈ 9,4cm
Le côté [PC] mesure 9,4cm

Soit FIG un triangle rectangle en F tel que FI=4cm et IG=8cm. Déterminer au millimètre près la longueur du côté [FG].
Solution :
Faire une figure à main levée et y inscrire ce qu’on connaît.

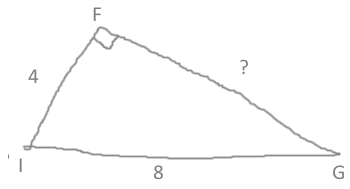
On cherche un côté et on connaît l’autre côté et l’hypoténuse dans un triangle rectangle.
Le triangle FIG est rectangle en F, d’après la propriété de Pythagore on a :
IG2 = FI2 + FG2
82 = 42 + FG2
64 = 16 + FG2
FG2 = 64 – 16 = 48
FG = √48
PC ≈ 6,9cm
Le côté [FG] mesure 6,9cm

I - Propriété de Thalès

1 - Enoncé

Dans un triangle ABC, I est un point du segment [AB] et J est un point du segment [AC].
SI (IJ) est parallèle à (BC)
ALORS
AI
AB
=
AJ
AC
=
IJ
BC

Cet énoncé est lié aux figures suivantes :

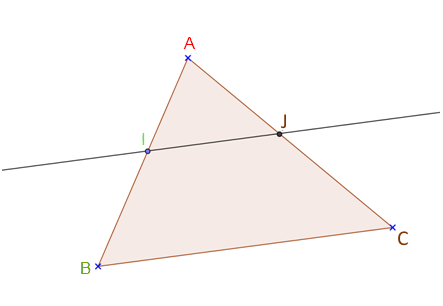
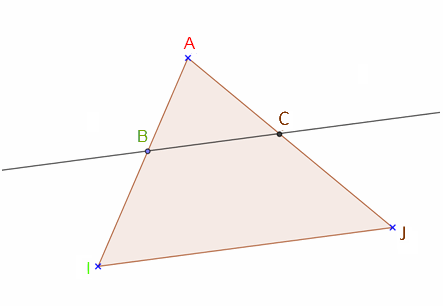
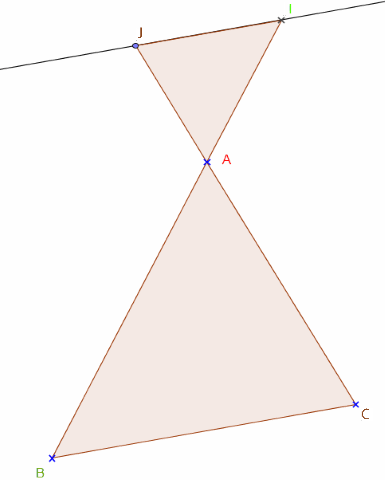
Ce théorème sert à calculer des longueurs dans un triangle quand il y a une droite parallèle à un côté.

2 - Application


Dans la figure ci-contre, les droites (AB) et (RT) sont parallèles.
On donne :
SA=4 cm, ST=15 cm, AB=2,4 cm et SR=7,5 cm.
Calculer SB et RT.

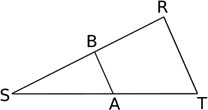
Solution :
Dans le triangle SRT, les droites (AB) et (RT) sont parallèles. Donc, d’après le théorème de Thalès on a :
SB
SR
=
SA
ST
=
BA
RT

SB
7,5
=
4
15
=
2,4
RT

Calcul de SB :
SB
7,5
=
4
15

SB =
4×7,5
15

SB =
30
15
= 2
Calcul de RT :
4
15
=
2,4
RT

RT =
2,4×15
4

RT =
36
4
= 9







3 - Cas particulier : milieu

Soit IPR un triangle tel que IP=7cm, IR=8cm et PR=9cm.
Soit A le milieu de [IP]. On appelle (d) la parallèle à (PR) passant par A. On appelle B l’intersection de (d) et (IR).
1 - Calculer (simplement) AI.
2 - En remarquant que (d) est parallèle à (PR), calculer IB.
3 - Que peut-on dire de B ?

Solution :
1 - AI =
IP
2
= 3,5
2 - Dans le triangle IPR, les droites (AB) et (PR) sont parallèles. Donc, d’après le théorème de Thalès on a :
IA
IP
=
IB
IR
=
AB
PR

3,5
7
=
IB
8
=
AB
9

IB =
3,5×8
7

IB =
28
7
= 4
3 - B est le milieu de [IR].

II - Proportionnalité – agrandissement – réduction.

1 - Proportionnalité dans le triangle

Dans un triangle ABC, I est un point du segment [AB] et J est un point du segment [AC].
SI (IJ) est parallèle à (BC)
ALORS les triangles AIJ et ABC sont proportionnels

Cet énoncé est lié à la figure suivante :

En effet, d’après la propriété de Thalès on a :
AI
AB
=
AJ
AC
=
IJ
BC

Donc le tableau suivant est un tableau de proportionnalité :
Triangle AIJAIAJIJ
Triangle ABCABACBC

2 - Agrandissement - réduction

Si deux figures sont proportionnelles, on dit que l’une est l’agrandissement ou la réduction de l’autre.

Plus précisément avec des coefficients MULTIPLICATIFS :
Si le coefficient de proportionnalité est supérieur à 1, on parle d’agrandissement.
Si le coefficient de proportionnalité est compris entre 0 et 1, on parle de réduction.

Triangle AIJ468
Triangle ABC6912
ABC est un agrandissement de AIJ car le coefficient de proportionnalité est égal à
3
2
.
AIJ est une réduction de ABC car le coefficient de proportionnalité est égal à
2
3
.

Dans un agrandissement/réduction, les angles, la perpendicularité et le parallélisme sont conservés.