G2 - Démontrer qu'un triangle est rectangle
Démontrer que deux droites sont parallèles

I - Réciproque ?

La propriété de Pythagore est un énoncé de la forme :
SI
ALORS


La réciproque d’un tel énoncé est un nouvel énoncé, construit sur le précédent, de la forme :
SI
ALORS

La réciproque peut être fausse bien que la propriété soit vraie et vice versa.

II - Démontrer qu'un triangle est rectangle

1 - La réciproque de Pythagore

Dans un triangle,
SI le carré du plus grand côté est égal à la somme du carré des deux autres côtés
ALORS ce triangle est rectangle.

Il faut connaître les longueurs des trois côtés du triangle pour appliquer la réciproque de Pythagore.

Le triangle dont les côtés mesurent 6cm, 4,5cm et 7,5cm est rectangle. En effet
7,5²=56,25
6²+4,5²=56,25

2 - Exercice-type

Démontrer que le triangle ci-dessous est rectangle.

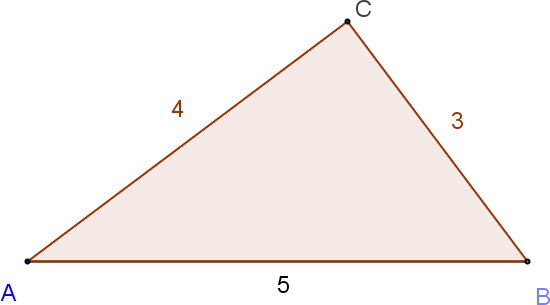
Solution :
Dans le triangle ABC, le plus grand coté est [AB] :
AB2 = 52 = 25
AC2 + CB2 = 42 + 32 = 16+9 =25
Donc AB2 = AC2 + BC2
D’après la réciproque de Pythagore le triangle est rectangle en C.

3 - Démontrer qu'un triangle n'est pas rectangle

Le triangle ci-dessous est-il rectangle ?

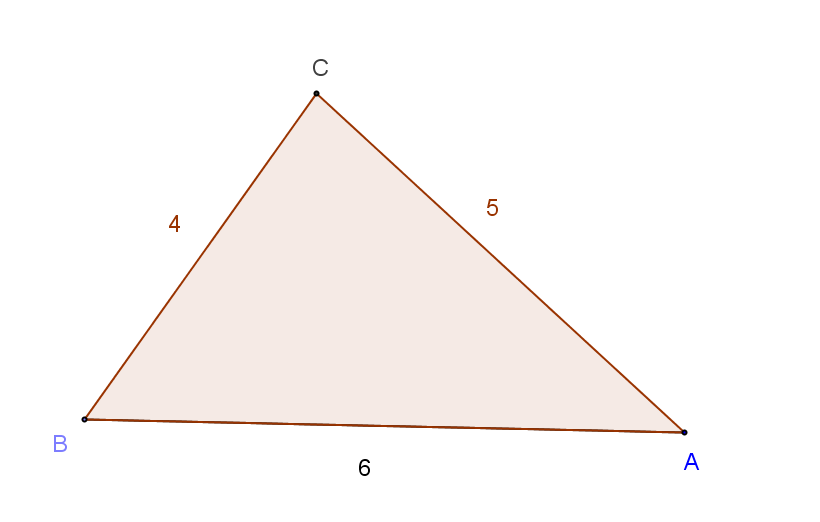
Solution :
Dans le triangle ABC, le plus grand coté est [AB] :
AB2 = 62 = 36
AC2 + CB2 = 52 + 42 = 25+16 =41
Donc AB2 ≠ AC2 + BC2
Le triangle n’est pas rectangle.

III - Démontrer que deux droite sont parallèles

1 - La réciproque de Thalès

Soit ABC un triangle. I est un point de (AB). J est un point de (AC).
SI
A,I,B sont alignés dans cet ordre
A,J,C sont alignés dans le même ordre
AI
AB
=
AJ
AC
ALORS les droites (IJ) et (BC) sont parallèles et
AI
AB
=
AJ
AC
=
IJ
BC
.

2 - Exercice-type

Les droites (LA) et (HT) sont-elles parallèles ?


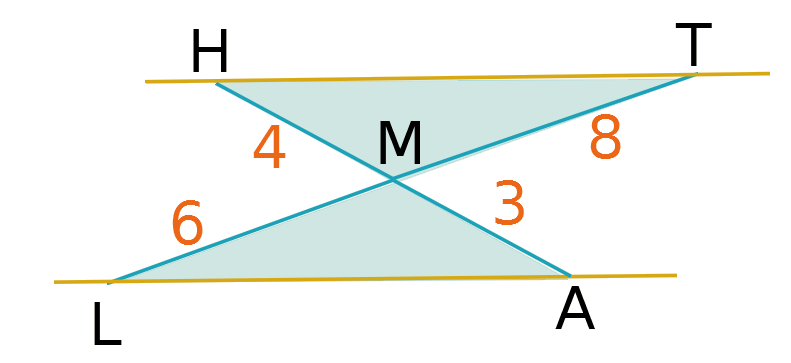
Les points A, M, H d'une part et les points L, M, T d'autre part sont alignés dans le même ordre.
De plus, on a
MH
MA
=
4
3
 et
MT
ML
=
8
6
=
4
3

On constate que
MH
MA
=
MT
ML
.
Donc, d'après la réciproque du théorème de Thalès, les droites (AL) et (HT) sont parallèles.

3 - Démontrer que deux droites ne sont pas parallèles

Sur la figure ci-dessous,

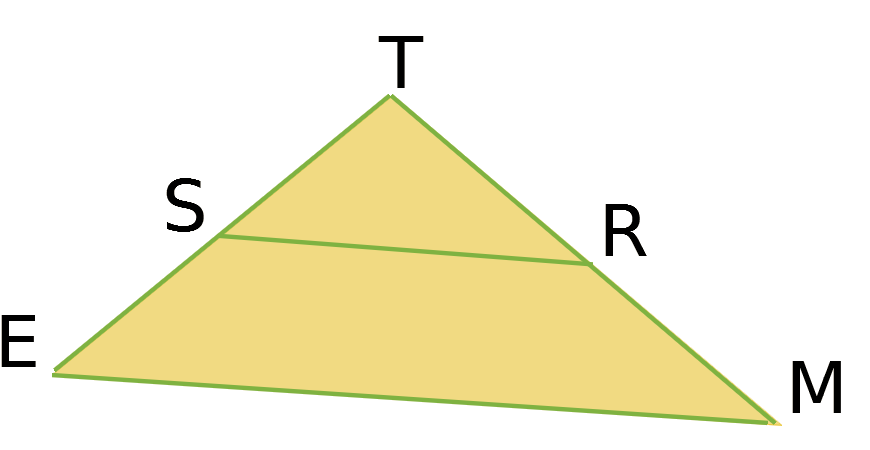
TR = 11 cm ; TS = 8 cm ; TM = 15 cm et TE = 10 cm.
Montre que les droites (RS) et (ME) ne sont pas parallèles.

Les droites (ES) et (MR) sont sécantes en T.
TS
TE
=
8
10
 et
TR
TM
=
11
12
.
On constate que
8
10
≠
11
12
Donc (RS) et (ME) ne sont pas parallèles.