cos(B) =
| AB |
| BC |
cos(C) =
| AC |
| BC |
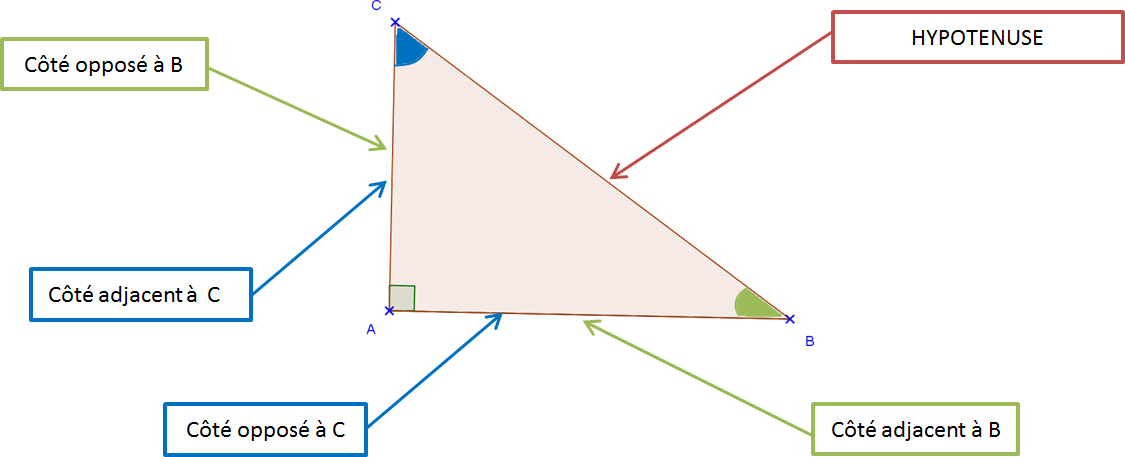
Dans un triangle ABC rectangle en A, on a :
cos(B) = AB BC
cos(C) = AC BC
On ne peut pas calculer le cosinus de l’angle droit.
cosinus = côté adjacent Hypoténuse
Soit UPS un triangle rectangle en P tel que UP=5cm et PUS=39°. Calculer US.
Solution :
On commence par faire un dessin à main levée.
Dans ce triangle, on connaît l'angle PUS et son côté adjacent PU, et on cherche l'hypoténuse US. On peut donc utiliser le cosinus.
Dans le triangle UPS rectangle en P on a :
cos(PUS) = UP US
On remplace ce qu’on connait :
cos(39°) = 5 US
Produit en croix :
= cos(39°) 1 5 US
US = 5×1 cos(39°)



US≈6,43
cosinus = côté adjacent Hypoténuse
sinus = côté opposé Hypoténuse
tangente = côté opposé côté adjacent
Comment choisir la «bonne» formule ?
On fait un bilan de la figure en terme d'angle, de côté adjacent, de côté opposé et d'hypoténuse. Puis on choisit la formule en fonction des mots qui apparaissent.
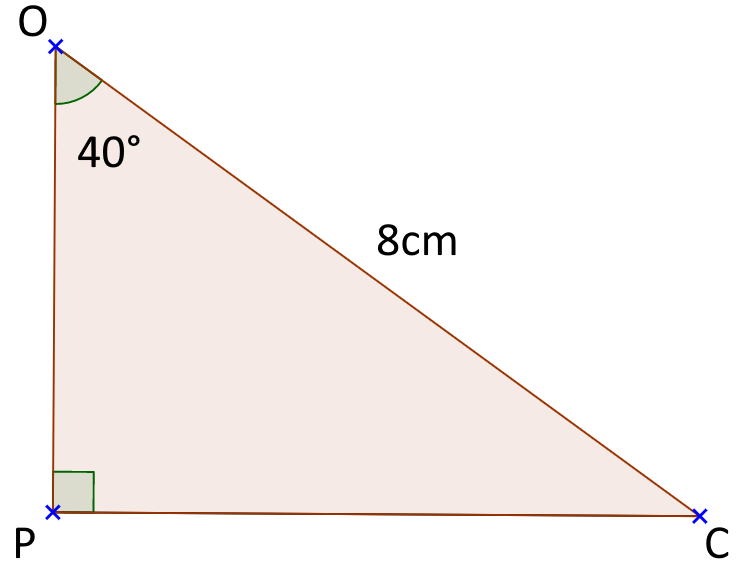 On veut calculer PC.
On veut calculer PC.
Bilan :
Dans le triangle OPC, on connait l'angle O et l'hypoténuse. On cherche le côté opposé.
On utilise donc le sinus de O.
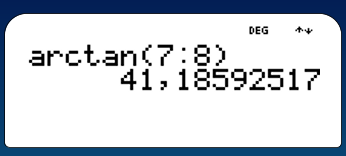
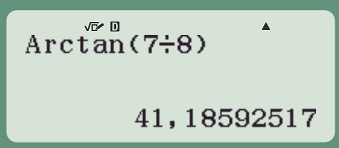
Soit OPC un triangle rectangle en P tel que OP=8cm et PC=7cm. Calculer POC.
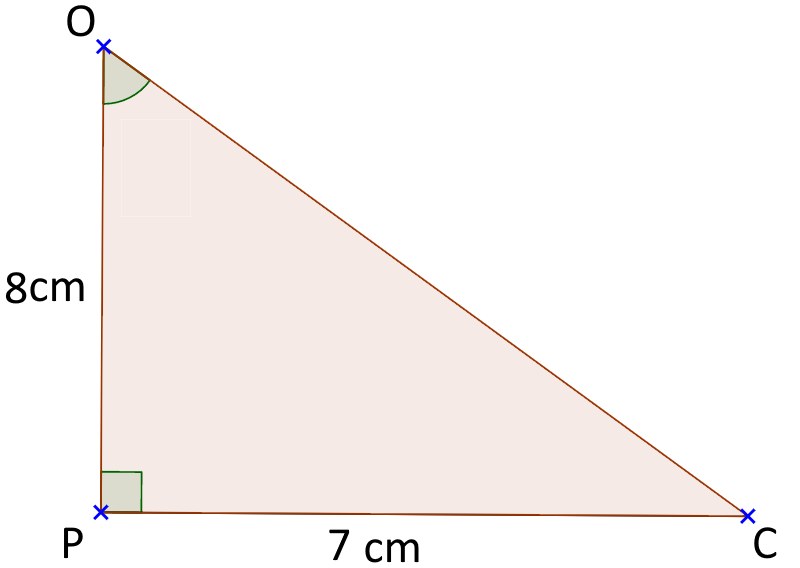
| PC |
| PO |
| 7 |
| 8 |