G5 – La sphère

I – La sphère

Soit O un point de l’espace et r un nombre positif ou nul.
La sphère de centre O et de rayon r est l’ensemble des points de l’espace dont la distance au point O vaut r.

Cela signifie que tous les points de la sphère sont à la même distance du point O.

Dans la figure ci-contre, OA = OM = r

La sphère est une surface : elle correspond à la « peau de l’orange ».

La boule de centre O et de rayon r est l’ensemble des points de l’espace dont la distance au point O est inférieure à r.
C'est l'intérieure de la sphère.

Soit une sphère de centre O et de rayon r.
Toute droite passant par le centre O coupe la sphère en 2 points diamétralement opposés.
On appelle grand cercle tout cercle de centre O et de rayon r.

Pour la Terre, l’équateur est un grand cercle.

[AB] est un diamètre.

II – Repérage sur la sphère

Sur une sphère, par un point M distinct des pôles il ne passe qu'un seul demi grand cercle (de centre O) passant par les pôles.
On l'appelle un méridien.

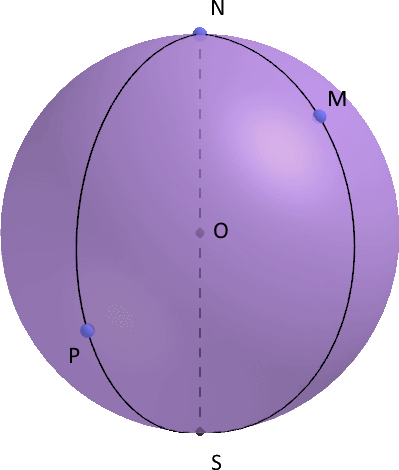
Un méridien est de diamètre [NS]

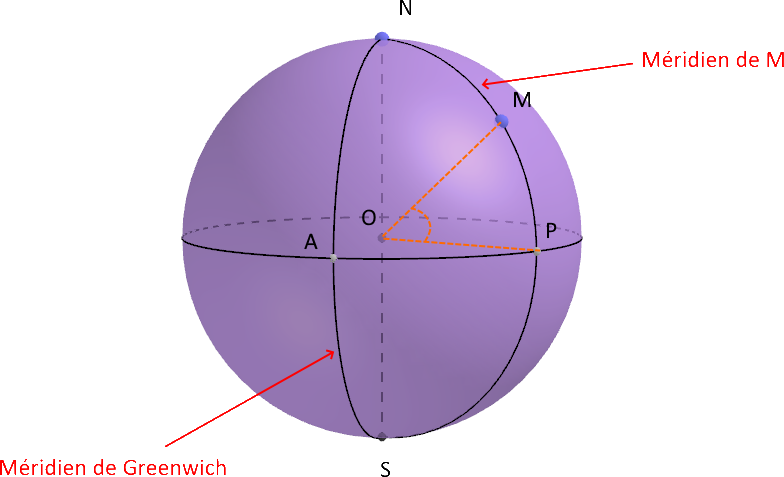
On repère les méridiens par rapport à un méridien-origine : le méridien de Greenwich.

La longitude du mériden de M (ou longitude de M) est la mesure de l'angle AOP. On indique aussi la direction (Est ou Ouest) par rapport au méridien de Greenwich.

La latitude de M est la mesure de l'angle POM suivie de l'indication Nord ou Sud.


Tous les points yant la même latitude définissent un parallèle qui est un cercle parallèle à l'équateur.



On obtient donc un système de coordonnées. Un point de la sphère est repéré par (Latitude; Longitude)


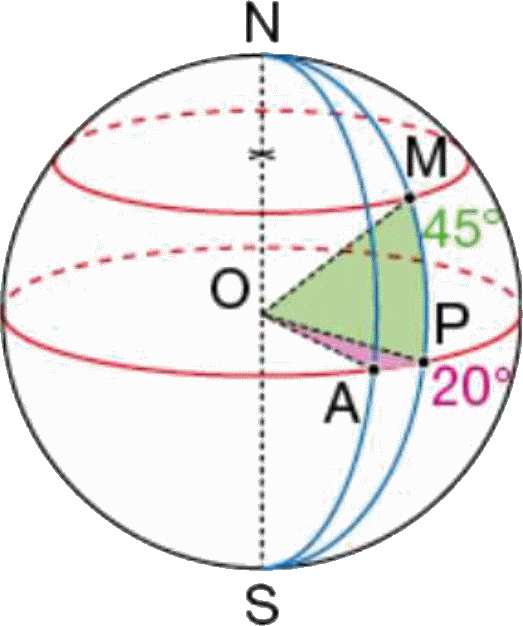Les coordonnées de M sur la sphère sont (20°E;45°N)


Indiquer les coordonnées des points P, V, N, U, Q S et Y :
P : (°,°)

V : (°,°)

N : (°,°)

U : (°,°)

Q : (°,°)

S : (°,°)

Y : (°,°)


III - Section

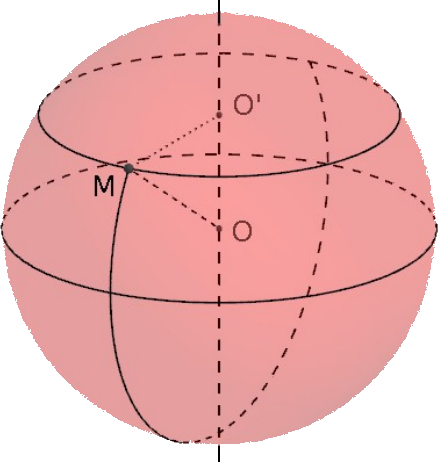
La section d’une sphère par un plan est un cercle.


Une sphère de rayon 4 m est coupée par un plan à 3 m de son centre. Quelle est la nature de la section obtenue et ses dimensions ?

La section d'une sphère par un plan est un disque.
Soient O le centre de la sphère et O' celui de la section.
En prenant un point M sur le bord de la section, on a le triangle OO'M qui est rectangle en O' Donc, d'après le théorème de Pythagore, on a :
OM² = O'M² + O'O²
4² = O'M² + 3²
O'M² = 16 − 9
O'M²=7
O'M = √7
O'M ≈ 2,65 m

IV - Volume et aire

On considère une sphère de rayon r. L'aire de sa surface vaut :
A = 4π × r2

Une tente igloo a la forme d’une demi sphère de 2 m de diamètre.
Quelle surface de tissus a t-on utilisé pour la fabriquer ? (tapis de sol compris)

A = Ademi-sphère + Asol
A =
4π × 12
2
+ π × 12
A = 2π + π
A = 3π
A ≈ 9,42 m²

On considère une boule de rayon r. Son volume vaut :
V =
4
3
× π × r3

Quel est le volume de l'igloo de l'exemple précédent ?

V =
4
3
× π × 13
V =
4
3
× π
V =
4π
3

V ≈ 4,189 m3