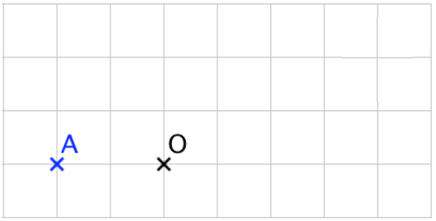
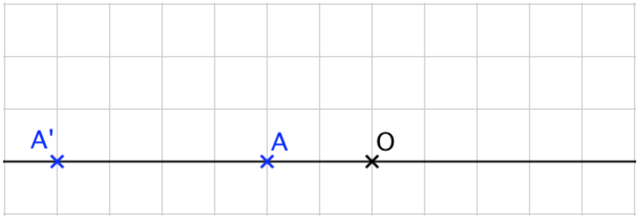
Construire l’image du point A par l’homothétie de centre O et de rapport 3.
 • On trace la droite (OA).
• On trace la droite (OA).• L’image A’ de A se trouve du même côté que A par rapport au point O.
• OA’ = 3 × OA.
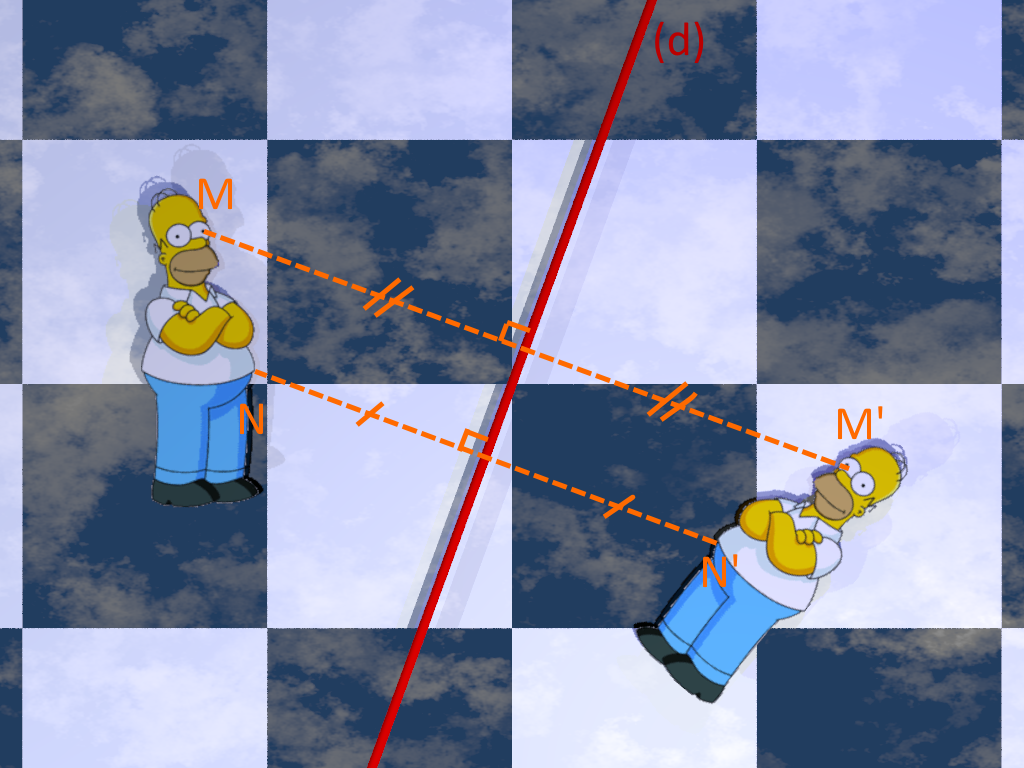
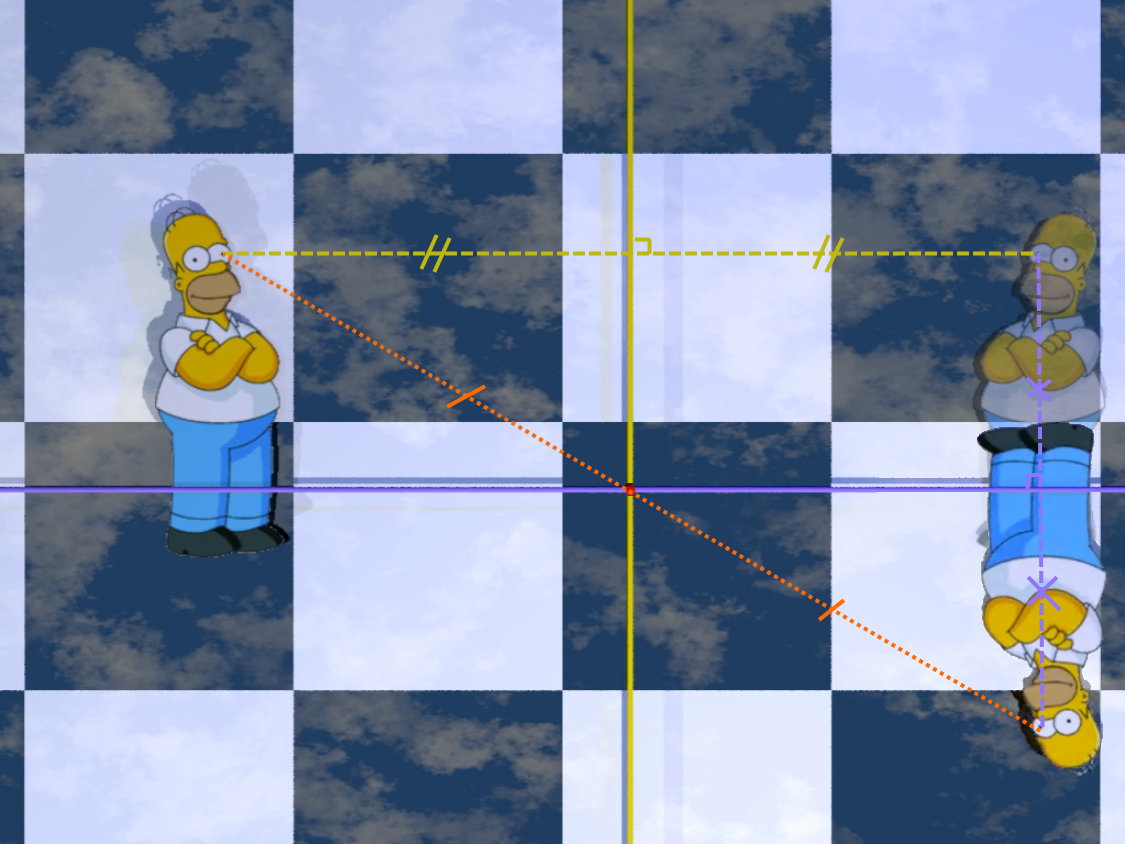
M et M’ sont symétriques par rapport à la droite (d) signifie que :
• (MM’) est perpendiculaire à (d),
• M et M’ sont à égale distance de (d).
Deux figures symétriques par symétrie axiale se superposent par un pliage le long de l’axe de symétrie.
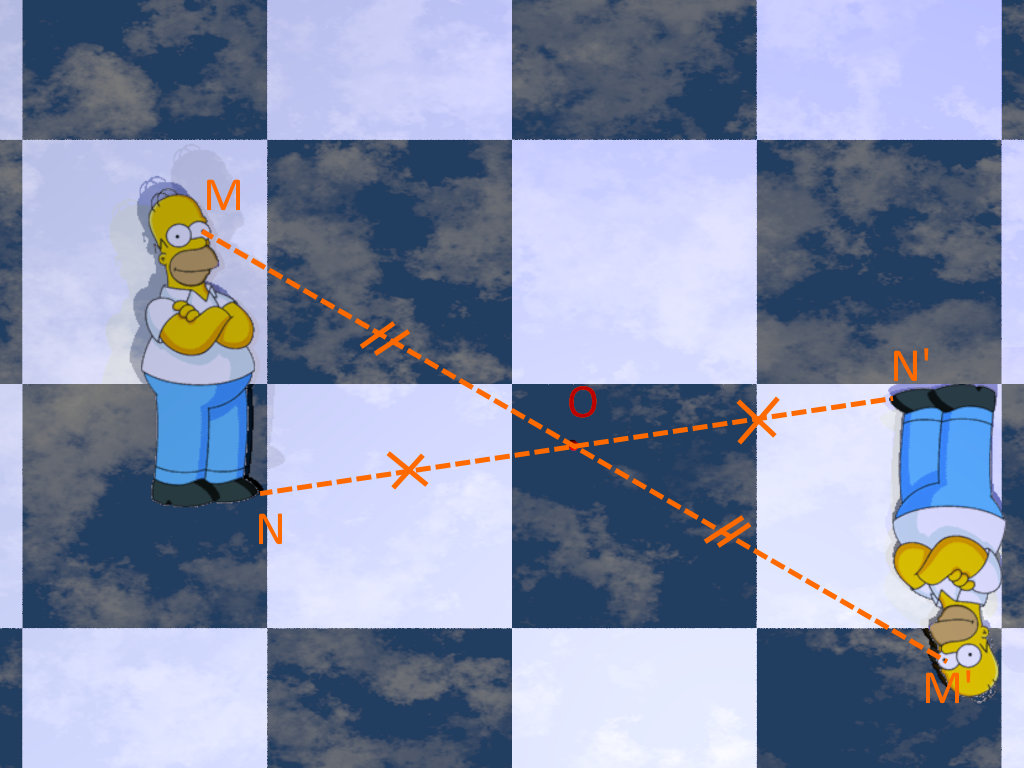
M et M’ sont symétriques par rapport au point O signifie que :
• M, O et M’ sont alignés,
• MO = OM’.
Un symétrie centrale de centre O correspond à 2 symétries centrales successives d'axes perpendiculaires et sécants en O
Cliquez pour lancer l'animation
Deux figures symétriques par symétrie centrale se superposent par un demi-tour autour du centre de symétrie.
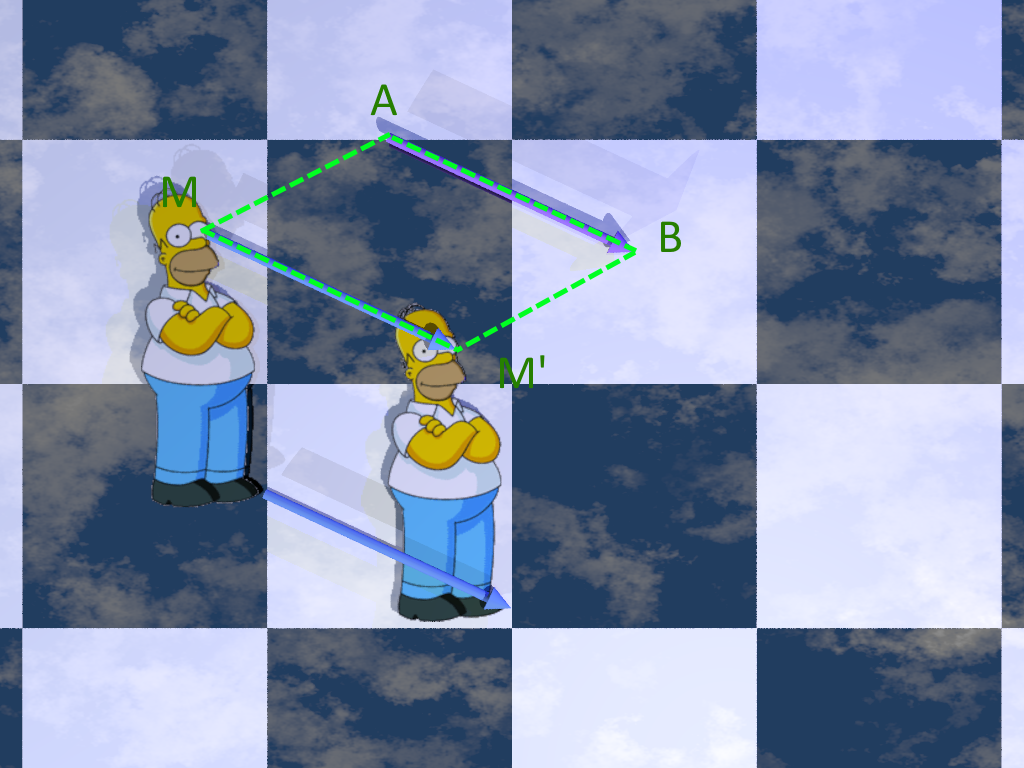
M’ est l’image de M par la translation qui envoie A en B signifie que :
• ABM’M est un parallélogramme.
Une translation de A vers B fait glisser une figure dans une direction, un sens et une longueur donnés par flèche AB
M’ est l’image de M par la rotation de centre O et d’angle 72° dans le sens inverse des aiguilles d’une montre signifie que :
• MOM'=72° de M vers M’ ,
• MO = OM’
Une rotation fait tourner une figure autour d’un point selon un angle.

M’ est l’image de M par l’homothétie de centre O et de rapport 0,47 signifie que :
• O, M et M’ sont alignés
• M et M’ sont du même côté par rapport à O.
• OM’ = 0,47 × OM

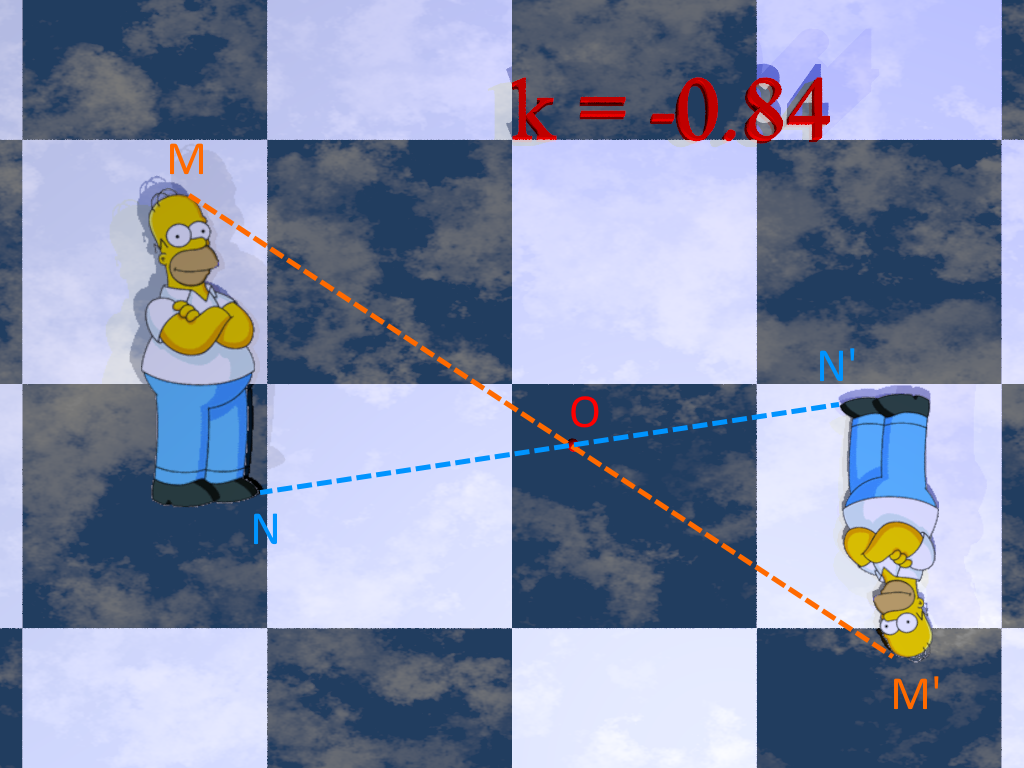
M’ est l’image de M par l’homothétie de centre O et de rapport -0,84 signifie que :
• O, M et M’ sont alignés
• M et M’ ne sont pas du même côté par rapport à O.
• OM’ = 0,84 × OM
Deux figures homothétiques sont une réduction ou un agrandissement l’une de l’autre.
Cliquez pour lancer l'animationConstruire l’image d’un point par une homothétie de rapport positif
Construire l’image du point A par l’homothétie de centre O et de rapport 3.
 • On trace la droite (OA).
• On trace la droite (OA).
• L’image A’ de A se trouve du même côté que A par rapport au point O.
• OA’ = 3 × OA.

Construire l’image d’un point par une homothétie de rapport négatif
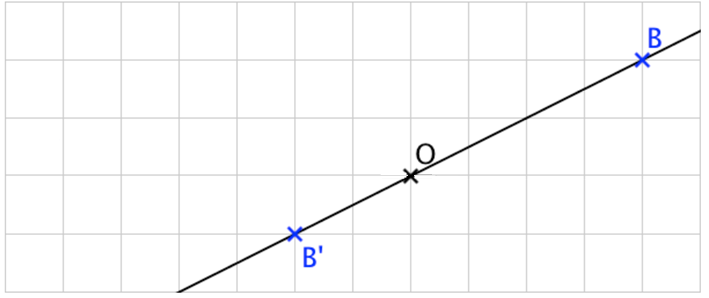
Construire l’image du point B par l’homothétie de centre O et de rapport -0,5.
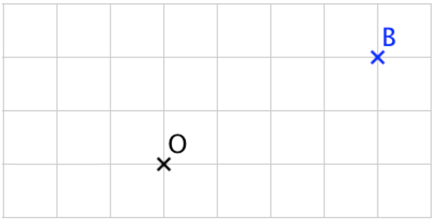 • On trace la droite (OB).
• On trace la droite (OB).
• L’image B’ de B se trouve de l’autre côté de B par rapport au point O.
• OB’ = 0,5 × OB.