Avec une TI-Collège Plus :
Avec une Casio Fx92+ Spéciale Collège :
On peut ensuite écrire la division :
Dans tout ce chapitre, on ne parle que de nombres entiers.
On dit qu’un nombre entier a est un diviseur d’un nombre entier b si
est un nombre entier.b a
5 est un diviseur de 20 car
= 4.20 5
8 n’est pas un diviseur de 30 car
= 3,7….
30 8
Cela revient à trouver un autre nombre entier c tel que b=a×c.
Déterminer tous les diviseurs d'un nombre
On veut trouver tous les diviseurs de 150.
On va écrire tous les produits de 2 nombres égaux à 150
150 = 1 × 150 C'est le premier à écrire
On va ensuite essayer tous les nombres inférieurs à 150 par ordre croissant pour le premier facteur
150 = 2 × 75 il n'y a aucun diviseur entre 75 et 150
150 = 3 × 50 il n'y a aucun diviseur entre 50 et 75
4 n'est pas un diviseur de 150
150 = 5 × 30 il n'y a aucun diviseur entre 30 et 50
150 = 6 × 25 il n'y a aucun diviseur entre 25 et 30
7, 8 et 9 ne sont pas des diviseurs de 150
150 = 10 × 15 il n'y a aucun diviseur entre 15 et 25
11, 12, 13 et 14 ne sont pas des diviseurs de 150
150 = 15 × 10 C'est terminé, on a testé tous les nombres possibles
Les divisuers de 150 sont 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75 et 150
Trouver tous les diviseurs de 48 ; de 100 ; de 19. Voir activité 1
On dit qu’un nombre est premier si ses seuls diviseurs sont 1 et lui-même.
7, 13, 47 sont premiers.
4, 27, 63 ne le sont pas.
1 n'est pas premier.
Un nombre entier peut toujours s'écrire comme un produit de facteurs premiers.
6 = 2 × 3
20 = 2 × 2 × 5 = 22 × 5
Décomposition d'un nombre entier en produit de facteurs premier
On veut décomposer 168
Etpae 1 : On commence par écrire 168 comme le produit de 2 nombres entiers (dont un est premier si possible rapidement)
168 = 2 × 84
Etape 2 : On écrit chaque facteur non premier du produit comme un produit de 2 facteurs (dont un est premier si possible rapidement)
168 = 2 × 84
168 = 2 × 4 × 21
Etape 3 : On recommence l'étape 2 jusqu'à ce qu'il n'y ait que des facteurs premiers dans le produit
168 = 2 × 84
168 = 2 × 4 × 21
168 = 2 × 2 × 2 × 3 × 7
Etape 4 : On écrit le résultats avec des puissances
168 = 23 × 31 × 71
On appelle diviseur commun aux nombres entiers a et b tout nombre entier qui est à la fois un diviseur de a et un diviseur de b.
Les diviseurs communs à 9 et 12 sont 1 et 3.
En effet :
Les diviseurs de 9 sont 1, 3 et 9.
Les diviseurs de 12 sont 1, 2, 3, 4, 6 et 12.
Le plus grand diviseur commun à plusieurs nombres est le plus grand de tous les diviseurs communs à tous ces nombres.
Le plus grand diviseur commun à 9 et 12 est noté PGCD(9;12). On a :
PGCD(9;12)=3
Quel est le PGCD de 28 et 35 ?
Diviseurs de 28 : 1, 2, 4, 7, 14, 28.
Diviseurs de 35 : 1, 5, 7, 35.
Donc PGCD(28;35)=7.
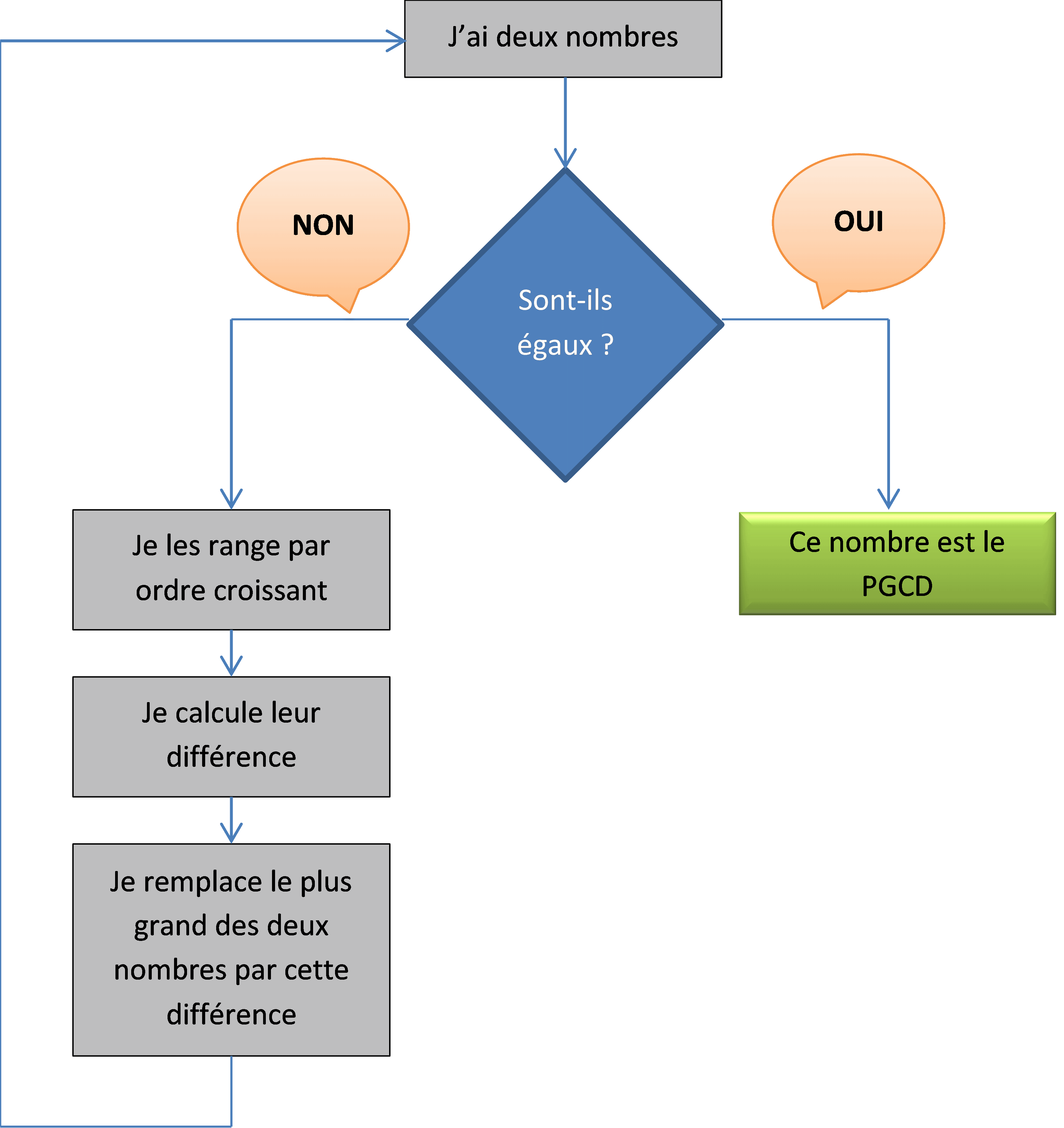
Calculer PGCD(189;693).
693-189=504
504-189=315
315-189=126
189-126=63
126-63=63
63-63=0
Donc PGCD(189;693)=63
attention à l’efficacité quand l’écart entre les deux nombres est grand. Pour calculer PGCD(693,15), il faudra effectuer un grand nombre de soustractions.
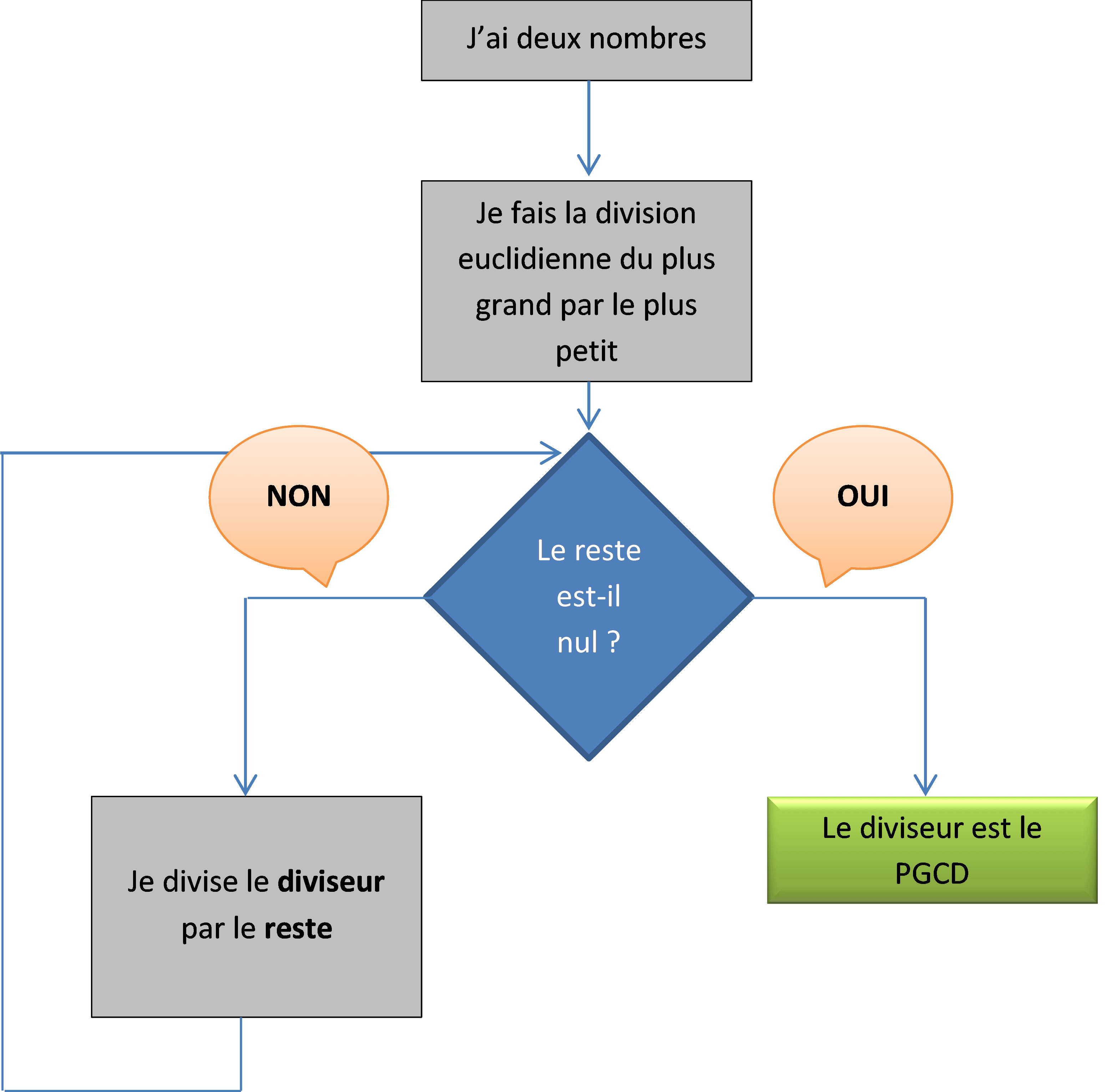
Calculer PGCD(189;693)
| 693 | 189 |
| 126 | 3 |
| 189 | 126 |
| 63 | 1 |
| 126 | 63 |
| 0 | 2 |
C’est souvent la méthode la plus efficace. Pour calculer PGCD(693;15), il faudra effectuer :
| 693 | 15 |
| 3 | 46 |
| 15 | 3 |
| 0 | 5 |
Effectuer la division euclidienne de 524 par 125
Avec une TI-Collège Plus :
Avec une Casio Fx92+ Spéciale Collège :
On peut ensuite écrire la division :
| 524 | 125 |
| 24 | 4 |
Un pâtissier dispose de 411 framboises et de 685 fraises. Afin de préparer des tartelettes, il désire répartir ces fruits en les utilisant tous et obtenir le maximum de tartelettes identiques.
Calculer le nombre de tartelettes et indiquer leur composition.
Solution : Le nombre de tartelettes doit diviser les nombres de framboises et de fraises et être le plus grand possible : c’est donc le pgcd.
| 685 | 411 |
| 274 | 1 |
| 411 | 274 |
| 137 | 1 |
| 274 | 137 |
| 0 | 2 |
Donc PGCD(411;685)=137 : Il pourra préparer 137 tartelettes.
Calcul du nombre de fruits par tartelette.
685÷137=5 : Il y aura 5 fraises par tartelette.
411÷137=3 : Il y aura 3 framboises par tartelette.
Simplifier (ou réduire) une fraction, c’est diviser le numérateur et le dénominateur par un même nombre pour les rendre plus simples (plus petits)
= 45 72
= 3×15 3×24 15 24
On dit qu’une fraction est irréductible quand on ne peut plus la simplifier, c’est-à-dire quand son numérateur et son dénominateur sont premiers entre eux.
= 45 72
= 3×15 3×24
= 15 24
= 3×5 3×8 5 8
| 75 |
| 105 |
| 5×15 |
| 5×21 |
| 15 |
| 21 |
| 3×5 |
| 3×7 |
| 5 |
| 7 |
Simplification d"un fraction par décomposition en produit de facteurs premiers
On veut simplifier
.900 750
On commence par décomposer 900 et 750 en produits de facteurs premiers
900 = 22 × 32 × 52
750 = 21 × 31 × 53
On écrit la fraction avec les décompositions
= 900 750 22 × 32 × 52 21 × 31 × 53
On simplie facteur premier par facteur premier
= 900 750
= 22 × 32 × 52 21 × 31 × 53
= 22-1 × 32-1 × 52-2 21-1 × 31-1 × 53-2 21 × 31 × 50 20 × 30 × 51
= 900 750
= 21 × 31 51 6 5
Pour rendre une fraction irréductible, il suffit de la simplifier par le pgcd de son numérateur et de son dénominateur.
Rendre
irréductible.396 360
PGCD(360;396)=36
= 396 360
= 36×11 36×10 11 10