N10 – Agrandissement, Réduction, Ratio
I – Agrandissement et réduction
Les longueurs sur une carte, un plan, un dessin " à l'échelle" sont proportionnelles aux longueurs réelles.
L'échelle est le coefficient de proportionnalité entre les distances représentées et les distances réelles, exprimées avec la même unité.
échelle = | distance sur la représentation |
| distance réelle |
Si l'échelle est un nombre inférieur à 1, la reproduction est une réduction par rapport à la réalité (carte, plan de construction, maquette...).
Si l'échelle est un nombre supérieur à 1, la reproduction est un agrandissement par rapport à la réalité (photographie sous microscope).
Sur une carte, 5 cm représentent 100 km, soit 10 000 000 cm.
L'échelle d'une carte s'exprime par une fraction de numérateur 1, à savoir ici :
=
Un insecte mesure 3 mm de longueur ; on le représente sur un dessin avec une longueur de 6 cm soit 60 mm. L'échelle du dessin est
= 20
.
Lors d'un agrandissement ou d'une réduction d'un objet à l'échelle k :
les longueurs de l'objet sont multipliées par k
l'aire de la surface de l'objet est multipliée par k2
le volume de l'objet est multiplié par k3
Un pavé a un volume V de 125 cm3. Ses dimensions sont multipliées par 2.
Quel est le volume du pavé agrandit ?
V’ = 125 × 23 = 125 × 8 = 1 000 cm3.
Le volume du pavé agrandit est 1 000 cm3.
II – Ratio
On dit que deux nombres a et b sont dans le ratio 2 : 3 si =
On dit que trois nombres a, b et c sont dans le ratio 2 : 3 : 4 si
= =
On peut également voir cela comme une situation de proportionnalité entre les quantités a, b et c.
«Il me faut 2 volumes de a pour 3 volumes de b pour 4 volume de c.»
Si a et b sont dans le ratio 2 : 3 alors on a aussi
=
.
Une télévision LED au format 16 : 9 a une diagonale de 65′′ (65 pouces) soit 163cm. Calculer la longueur et la largeur de l’écran de cet télévision.
Dire que la longueur L et la largeur l de cette télévision sont dans un ratio 16 : 9 signifie que = .
Cela signifie aussi que les grandeurs suivantes sont proportionnelles :
| Grandeurs réelles | L | l |
| Ratio | 16 | 9 |
Ainsi on peut considérer que l’écran de télévision est un agrandissement d’un écran de longueur 16cm et de largeur 9cm.
Calculons la diagonale de cet écran miniature.
D’après le théorème de Pythagore, la diagonale d vérifie :
d2 = 162 + 92
d2 = 337
d = √337
d ≈ 18,357
Ainsi, les grandeurs suivantes sont proportionnelles :
| Grandeurs réelles | L | l | 163cm |
| Ratio | 16 | 9 | 18,357 |
Finalement on obtient :
L = ≈ 142cm
l = ≈ 80cm
Cette télévision a une longueur d’environ 142cm et une largeur de 80cm
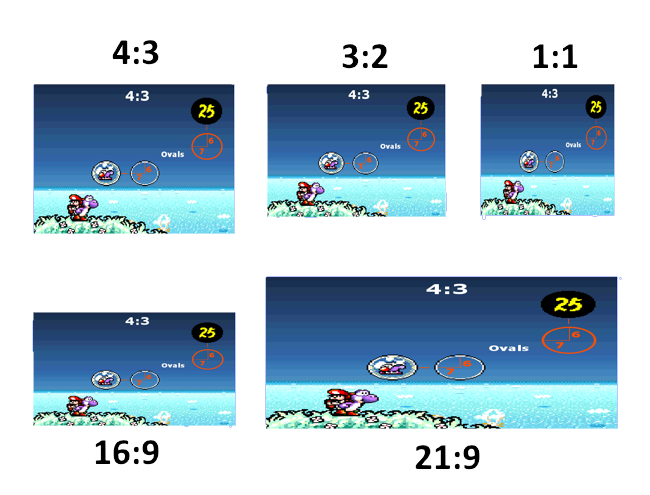
Voici une image prévue pour un affichage au ratio 4:3 projetée dans différents ratio :