N5 – Généralités sur les fonctions

I – Définition

Une fonction numérique est un ensemble de processus qui associe à un objet qui varie un unique nombre.

Object → → nombre

À Auxerre, le température dépend de la date (et de l'heure) :

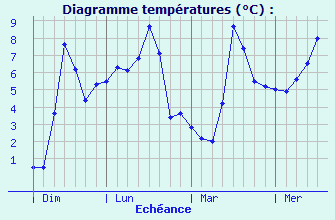
Date → → Température C'est une fonction

À chaque date correspond une seule température, mais pour une température donnée, il peut correspondre plusieurs dates.

Voici le relevé de note de Madoka en mathématiques pour le premier trimestre.
Devoir n° 1 2 3 4 5 6 7
Note 14 16 16 12 9 18 19

Numéro du devoir → → Note C'est une fonction

Voici un relevé de notes d'une classe de troisième pour le brevet
MathématiquesFrançaisHistoire Géographie
Max12815
Madoka151618
Henri7917
Joshua15511

Note →
→Nom
 Ce n'est pas une fonction.

Soit f une fonction. On note généralement x la variable. Le nombre qui résulte de l'application de la fonction f à chaque valeur de x est noté f(x). On note:
f : x ⟼ f(x)

On peut noter la variable comme on veut :
f : 😎 ⟼ f(😎)

f(x) se lit «f de x»

Le nombre f(x) est appelé l'image de x par f.

II – Représentation graphique

1 – Tableau de valeurs

On peut dresser un tableau donnant les valeurs du cosinus d'un angle en fonction de l'angle avec la calculatrice :
Angle en ° 0 10 20 30 40 50 60 70 80 90
cosinus 1 0,98 0,94 0,87 0,77 0,64 0,5 0,34 0,17 0
Le cosinus varie quand l'angle varie : c'est une fonction. cos : α ⟼ cos(α)

On appelle tableau de valeur de la fonctionle tableau suivant :
x a b c d
f(x) f(a) f(b) f(c) f(d)
où les valeurs a, b, c et d sont des nombres.

2 – Représentation graphique

La représentation graphique d'une fonction est une courbe qui représente l'évolution de f(x) quand x varie. La variable x est repérée en abscisse et la valeur correspondante de f(x) en ordonnée.

Chaque point de la courbe a des coordonnées qui sont liées en elles.
Si un point M de la courbe a pour abscisse a, son ordonnée est alors f(a). On a alors M(a;f(a))

Soit M(x;y) un point du plan.
• soit y = f(x) et alors le point M appartient à la courbe de f
• soit y ≠ f(x) et alors le point M n'appartient pas à la courbe de f.

Pour chaque point de la courbe d'une fonction, son ordonnée est l'image de son abscisse.

III – Forme algébrique

On appelle forme algébrique d'une fonction f l'expression qui permet de calculer explicitement f(x) à partir de x. On dit que f(x) est défini en fonction de x.
C'est une formule.


• Soit g la fonction définie par g(x) = 2x + 1
• h : x ⟼ 4x2 - 12x +9

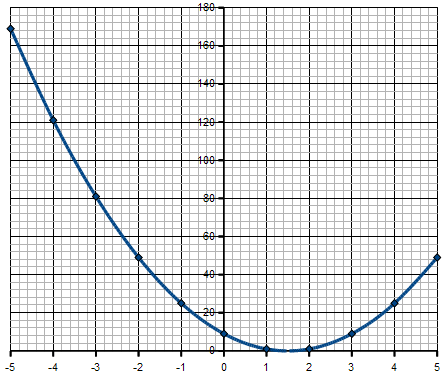
Soit h la fonction définie par h(x) = 4x2 - 12x +9. Tracer le courbe représentative de h.

On dresse un tableau de valeurs :
x -5 -4 -3 -2 -1 0 1 1,5 2 3 4 5
h(x) 169 121 81 49 25 9 1 0 1 9 25 49

On trace la courbe correspondant au tableau.

IV – Image et antécédent

Dans ce paragraphe, h est la fonction définie par h(x) = 4x2 - 12x + 9.

1 – Image

a – Graphiquement

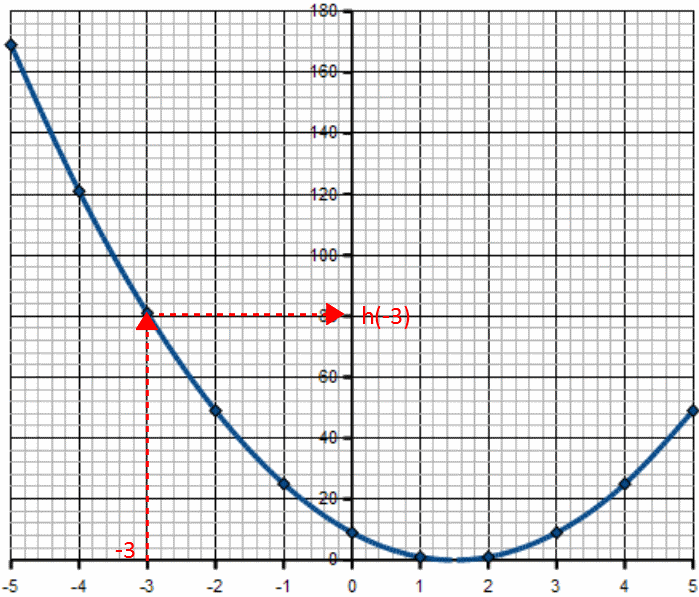
Déterminer l'image de -3 par h On peut aussi poser la question de la manière suivante : « Déterminer graphiquement»

Pour un nombre donné, il n'y a qu'une seule image (si elle existe)

b – Par le calcul

Déterminer l'image de -3 par h
Il faut calculer h(-3) c'est-à-dire remplacer x par -3 dans l'expression h(x).
h(-3) = 4 × (-3)2 - 12 × (-3) + 9 = 81
L'image de -3 par h est 81.

2 – Antécédent

a – Définition

Soit f une fonction et y un nombre donné.
On dit qu'un nombre x est un antécédent de y par f si f(x) = y.

On sait que (-3) est un antécédent de 81 par h car h(-3) = 81.

b – Graphiquement

Déterminer les antécédents de 40 par h. 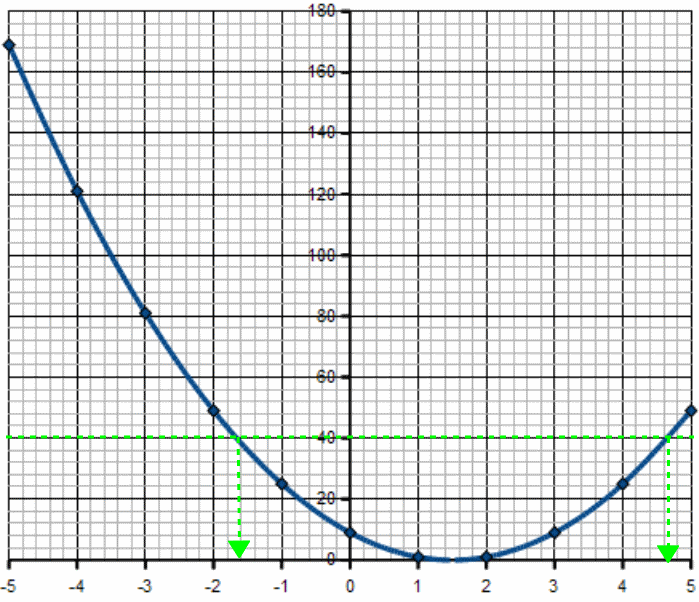40 a deux antécédents environ égaux à -1,6 et 4,6.

Pour un nombre donné, il peut y avoir plusieurs antécédents ou ne pas en avoir.

c – Par le calcul

Déterminer les antécédents de 40 par h.
Cela revient à trouver tous les nombres x tels que h(x) = 40, c'est à dire résoudre l'équation 4x2 - 12x + 9 = 40

Cette équation n'est pas toujours résoluble en troisième.

V – Exercice type Brevet

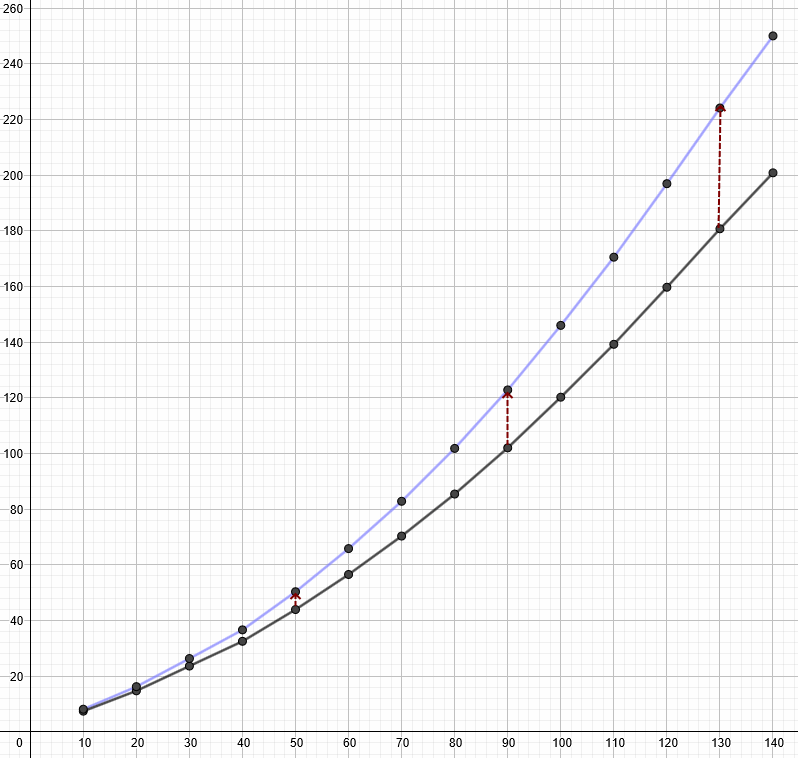
Distance de freinage (source : Eduscol)
La distance d'arrêt DA est la distance qu'il faut à un véhicule pour s'arrêter. Elle dépend de la vitesse et se décompose en la somme de la distance parcourue pendant le temps de réaction DTR et de la distance de freinage DF.
DA = DTR + DF a. Donne des paramètres dont dépend DTR.
b. Donne des paramètres dont DF est fonction.
On rappelle que V =
D
t
 où V est la vitesse et D la distance parcourue pendant le temps t.
c. Pour un conducteur en bonne santé, le temps de réaction est évalué à 2 s. Calcule la distance DTR (en m) pour un véhicule roulant à 50 km/h puis à 130 km/h.
d. Pour un conducteur en bonne santé, exprime la distance DTR (en m) en fonction de la vitesse V en km/h.
e. Recopie le tableau suivant qui donne DF, DTR et DA (en m) en fonction de la vitesse V (en km/h) sur route sèche.
V en km/h 10 20 30 40 50 60 70 80 90 100 110 120 130 140
DF(V) 1,8 3,6 6,9 10,3 16,1 23,2 31,4 41 52 64,6 78,1 93 108,5 123
DTR(V)
DA(V)
DFM(V)
DAM(V)
f. Sur route mouillée, la distance de freinage augmente de 40%. Calcule la distance de freinage sur route mouillée, DFM(50), d'un véhicule roulant à 50 km/h.
Complète le tableau en calculant DFM(v).
g. Complète le tableau en calculant la distance d'arrêt d'un véhicule sur route mouillée DAM(v).
h. Sur une feuille de papier millimétré, représente la distance d'arrêt d'un véhicule sur route sèche et sur route mouillée en fonction de la vitesse. (Tu prendras en abscisse 1 cm pour 10 km/h et en ordonnée 1 cm pour 20 m.)
i. Détermine, sur le graphique, l'augmentation de la distance d'arrêt entre une route sèche et une route mouillée pour les vitesses de 50 km/h ; 90 km/h et 130 km/h.
j. Où se positionnerait la courbe de la distance d'arrêt sur une route verglacée par rapport aux deux courbes précédentes ?

Solution : (Cliquez ici pour voir)