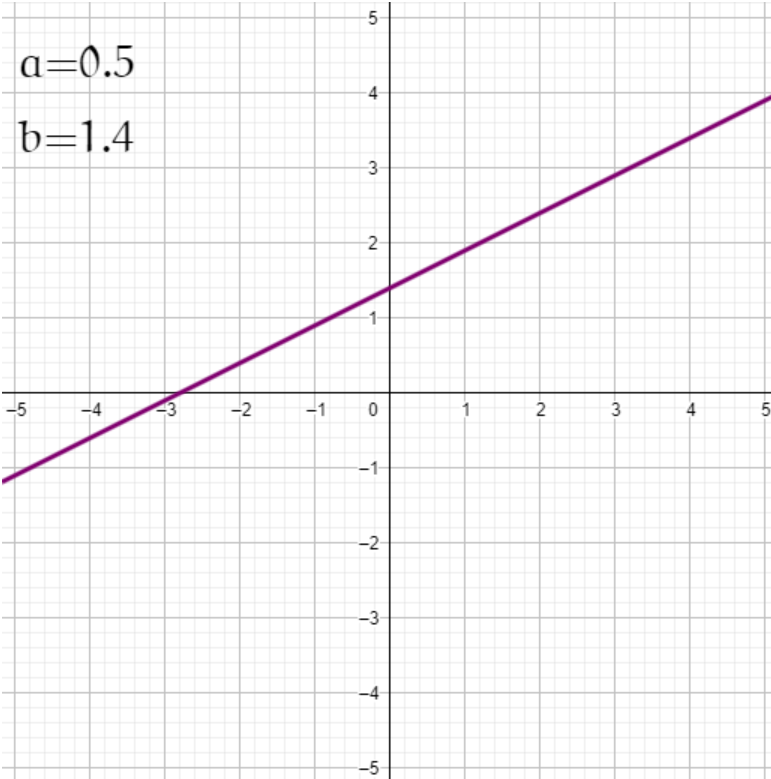
Modififiez les valeurs de a et b et observez :
a =
b =
On appelle fonction affine f toute fonction qui, à tout nombre noté x, associe le nombre f(x) défini par :
f(x)=a × x + boù a et b sont deux nombres connus.
Soient les fonctions f, g et h telles que :
f(x) = 5x − 2 g(x) = x² − 4 h(x) = 2x
f est une fonction affine où a = 5 et b = -2.
g n'est pas une fonction affine à cause de x².
h est une fonction affine où a = 2 et b = 0.
La représentation graphique d'une fonction affine est une droite

Pour tracer la représentation graphique d'une fonction affine, 2 points suffisent.
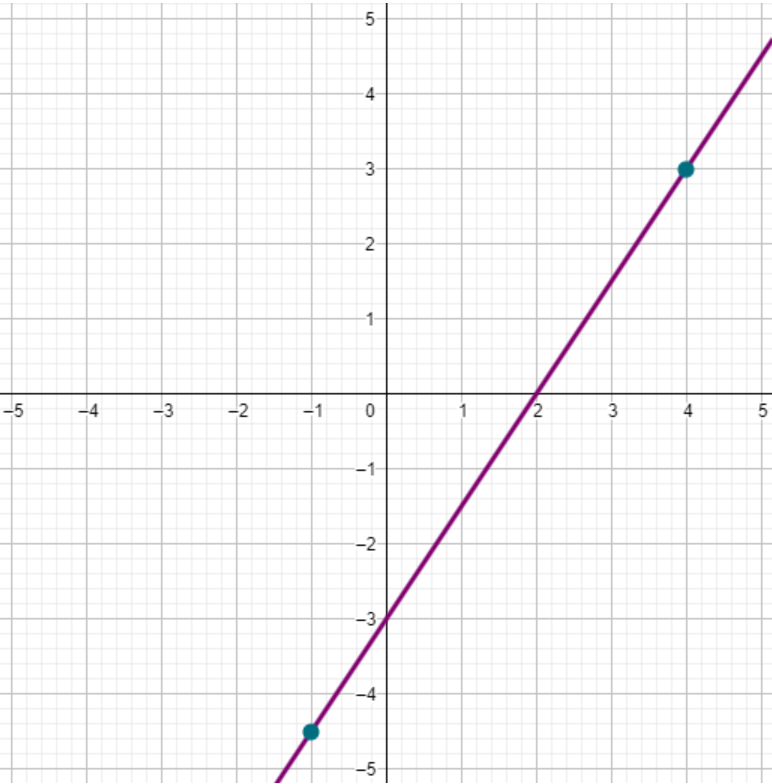
Soit f la fonction affine définie par f(x)=1,5x-3.
| x | -1 | 4 |
| f(x) | -4,5f(-1) = 1,5 × (-1) - 3 = -4,5 | 3f(4) = 1,5 × 4 - 3 = 3 |
Soit f(x)=a × x + b une fonction affine. On a toujours f(0)= b.
Soit f la fonction affine définie par f(x)=1,5x-3 : f(0)= 1,5 × 0 - 3 = -3
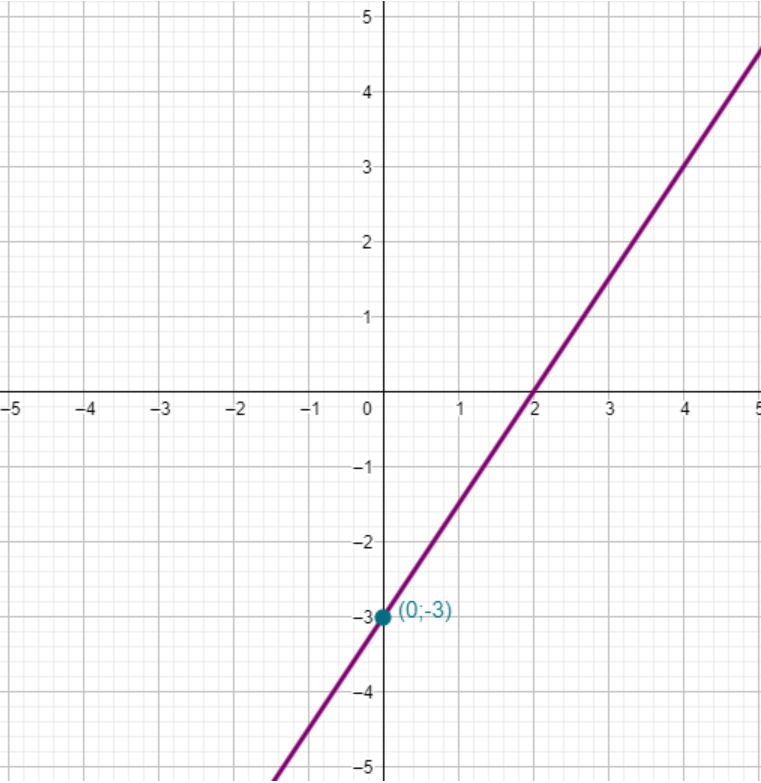
Soit f(x)=a × x + b une fonction affine.
b est appelé l'ordonnée à l'origine
C'est l'ordonnée du point d'intersection de la droite représentant la fonction affine et de l'axe des ordonnées.
Soit f la fonction affine définie par f(x)=1,5x-3 et g la fonction affine définie par g(x)=2x-3.
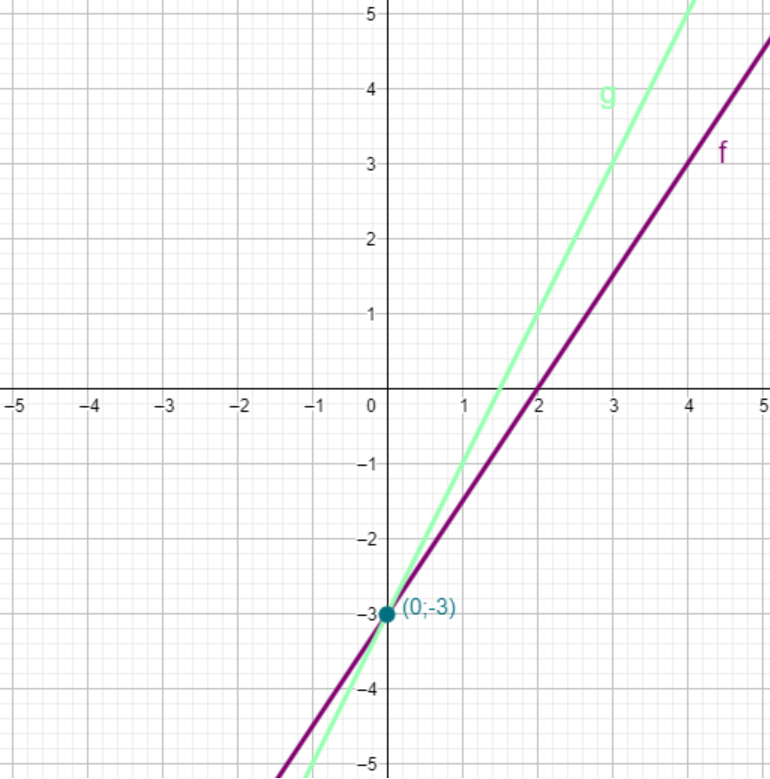
Les deux fonctions ont la même ordonnée à l'origine -3. Elles se coupent donc au point de coordonnées (0;-3).
On voit que le coefficient ade g (qui vaut 2) est supérieur à celui de f (qui vaut 1,5) : il détermine l'inclinaison de la droite.
Soit f(x)=a × x + b une fonction affine.
a est appelé la pente de la fonction ou son coefficient directeur.
Si a>0, la droite monte.
Si a<0, la droite descend.
Si a=0, la droite est horizontale.
Si deux fonctions affines ont la même pente, alors les droites qui les représentent sont parallèles.
Si deux fonctions affines ont des pente différentes, alors les droites qui les représentent sont sécantes.
Soit f et g deux fonctions.
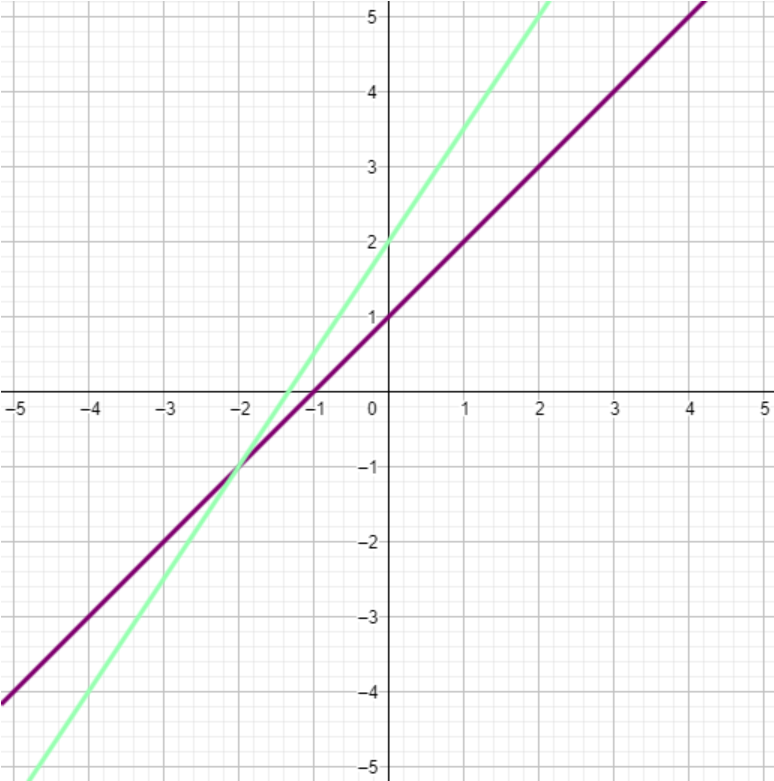
Soit f une fonction et m un nombre.
un antécédent de m par f est un nombre t qui a pour image m.
On a donc f(t) = m.
Un nombre peut avoir plusieurs antécédents comme il peut ne pas en avoir.
Soit f une fonction affine de pente différente de 0 et m un nombre.
m a un unique antécédent par f.
Pour déterminer l'antécédent d'un nombre m par une fonction affine f par un calcul, il suffit de résoudre l'équation f(x) = m.
Soit f la fonction définie par f(x) = -2x + 9. Déterminer l'antécédent de 12 par f.
Il faut résoudre l'équation f(x) = 12.
On commence par remplacer f(x) par son expression -2x + 9, puis on résout l'équation :
-2x + 9 = 12
-2x + 9 - 9 = 12 - 9
-2x = 3
= -2x -2 3 -2
x = -3 2
On vérifie :
f(-
) = -2×(-3 2
) + 9 = 12
3 2
Une droite non parallèle à l'axe des ordonnées est la représentation graphique d'une fonction affine.
Déterminer l'expression d'une fonction affine
Soit A(-4;1) et B(4;3) deux point dans un repère. Déterminer la fonction affine f qui a pour représentation la droite (AB).
Comme f est une fonction affine, elle est de la forme f(x) = ax + b. Déterminer f revient donc à déterminer a et b.
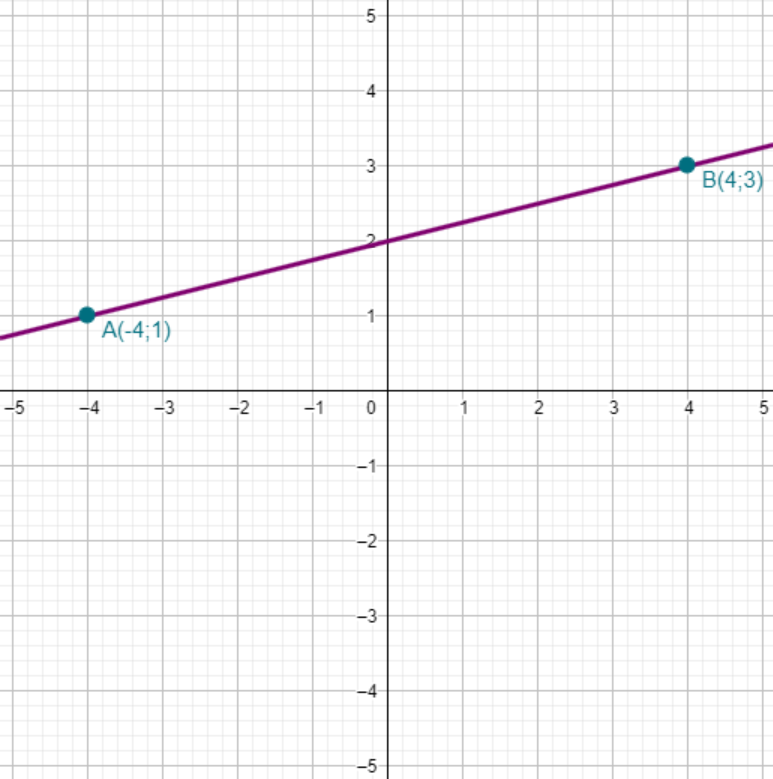
Calcul de a
Si on note A(xA;yA) et B(xB;yB), on a la formule
a =
.yB - yA xB - xA
ici on a A(-4;1) et B(4;3)
a = 3 - 1 4 - (-4)
a = 2 8
a =
= 0,251 4
On a donc une formule partielle : f(x) = 0,25×x + b
Détermination de b
Rappel : Quand un point est sur la représentation d'une fonction, son ordonnée est l'image de son abscisse par la fonction.
Donc avec les coordonnées de A (ou celles de B) :
f(-4) = 1.
On remplace ensuite f(-4) en "injectant" la formule partielle : f(-4) = 0,25×(-4) + b = -1 + b.
On obtient :
-1 + b = 1 Ce qui est une équation d'inconnue b qu'on va résoudre
-1 + b +1 = 1 +1
b = 2
On a donc une formule : f(x) = 0,25x + 2 quand vérifie sur le graphique.
On appelle fonction linéaire f toute fonction qui, à tout nombre noté x, associe le nombre f(x) défini par :
f(x)=a × x où a est un nombre connu.
C'est une fonction affine où l'ordonnée à l'origine est égale à 0.
La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère.
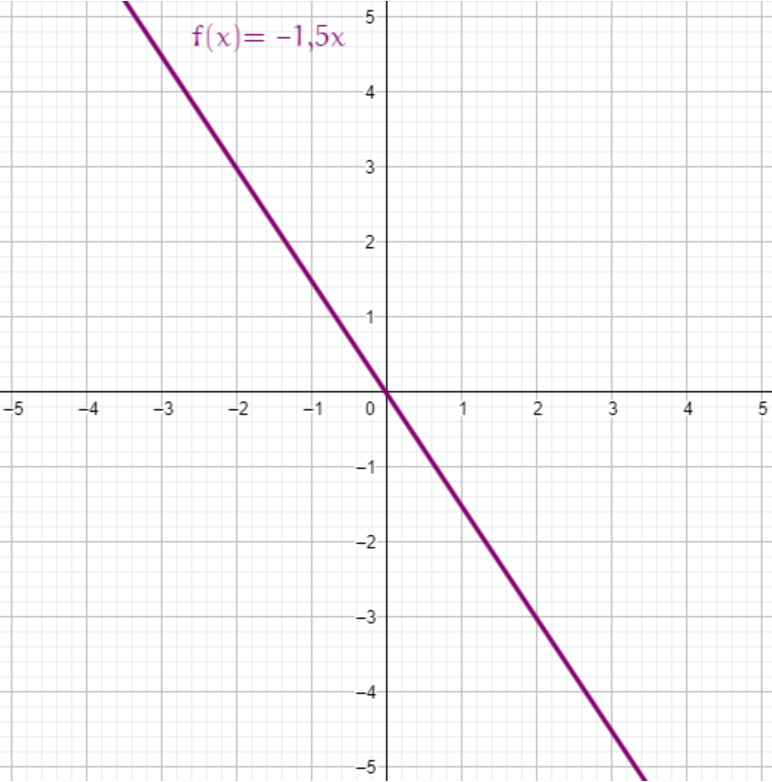
Pour tracer la représentation graphique d'une fonction linéaire, 1 point suffit puisque la droite passe forcément par l'origine.
Soit f la fonction linéaire définie par f(x) = -1,5x.
| x | 3 |
| f(x) | 3,5f(3) = 1,5 × 3 = 4,5 |
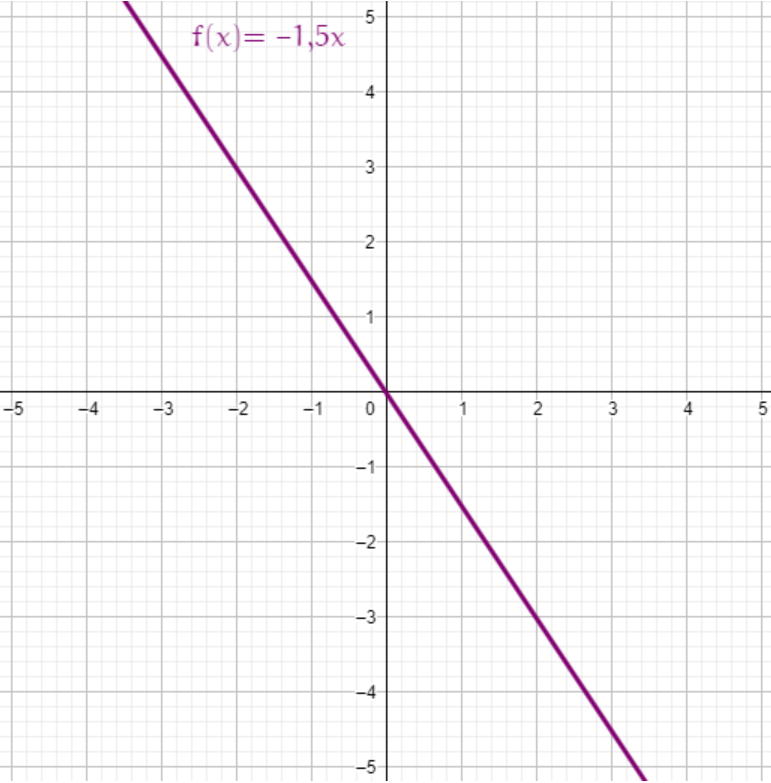
Un fonction linéaire représente une situation de proportionnalité
| n | 10 |
| PA(n) | 480 |
| n | 0 | 10 |
| PB(n) | 45 | 465 |