D1 – Proportionnalité.

I - Grandeurs proportionnelles

Deux grandeurs sont proportionnelles si elles sont liées par une multiplication.

• Quand une voiture roule à une vitesse constante, le temps de parcours et la distance parcourue sont proportionnels.
• La masse d'un homme n'est pas proportionnelle à son âge.

Quand deux grandeurs sont proportionnelles, si on double la valeur de l'une, on double la valeur de l'autre.

Quand deux grandeurs sont proportionnelles, la multiplication qui les lie est appelée le coefficient de proportionnalité.

II - Tableau de proportionnalité

1 - Qu'est-ce qu'un tableau de proportionnalité ?

Un tableau de proportionnalité est un tableau regroupant des valeurs de deux grandeurs proportionnelles.

Un piéton marche à 6 km⁄h. Il relève toutes les 5 minutes la distance qu'il à parcourue grâce à son GPS :

Temps en minutes	0	5	10	15	20	25	30	35	40
Distance en m	0	500	1000	1500	2000	2500	3000	3500	4000

un tableau est un tableau de proportionnalité si, pour chaque colonne, on « passe » de la première à la seconde ligne en multipliant par le même nombre : le coefficient de proportionnalité.

2 - Comment calculer le coefficient de proportionnalité ?

Le coefficient de proportionnalité se calcule dans n'importe quelle colonne du tableau :

Temps en minutes	5
Distance en m	500

On divise le nombre qui est au bout de la flèche par celui qui est au début de la flèche.
Le coefficient est égal à 500÷5=100.

on peut aussi calculer le coefficient dans l'autre sens :

Temps en minutes	5
Distance en m	500

Le coefficient est égal à 5÷500=0,01. Cela revient à diviser par 100.

3 - Remplir un tableau de proportionnalité

a - Avec le coefficient de proportionnalité

La prime annuelle d’un vendeur est proportionnelle au montant des ventes qu’il a réalisées pendant l’année. Le directeur du magasin utilise le tableau suivant pour verser les primes à ses vendeurs. Aide-le à compléter les cases colorées.

• 8000÷500=16 : on multiplie par 16 pour passer de la seconde à la première ligne.
• On divise par 16 dans l'autre sens.

b - Opérations sur les colonnes

dans un tableau de proportionnalité, on peut :
- Ajouter ou soustraire deux colonnes pour en obtenir une troisième.

5	+	10	=	15
6		12		18

- Multiplier ou diviser une colonne par un nombre pour en obtenir une seconde

3 ×	5	=	15
	6		18

On considère le tableau suivant :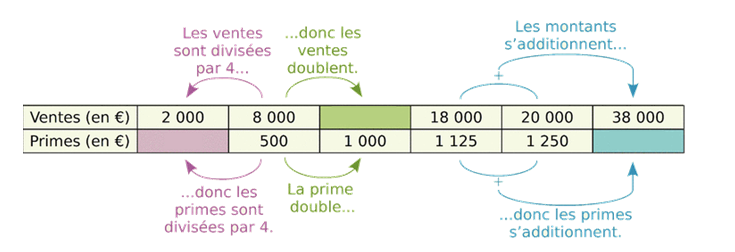

On utilise cette méthode lorsque le coefficient de proportionnalité n'est pas un nombre décimal, ou pour simplifier les calculs.

c - Produit en croix

- On choisit deux colonnes dont une complète.

2000	8000
	50

- On multiplie les nombres qui sont sur la diagonale complète et on divise le résultat par le nombre qui est sur la diagonale incomplète. A=2000×5÷8000=125

B=8000×1000÷500=16000

C=1125×38000÷18000=2375

III - Pourcentages

1 - Définition

Un pourcentage est un nombre qui permet de comparer une part par rapport à 100.

50% des élèves d'une classe représente la moitié des élèves de la classe.

2 - Calculer un pourcentage

Pour exprimer simplement un pourcentage, il suffit de placer clairement le problème dans un tableau de proportionnalité à quatre nombres, dont l'un est 100.

Sur 835 visiteurs d'un château en une journée, 144 sont des étrangers; Quel est le pourcentage de visiteur étranger ?

3 - Pourcentage de variation

Un pantalon coutait 59€ avant les soldes. Son prix est alors réduit de 30%. Quel est son nouveau prix ?

En deux étapes :
- Calculer d'abord la réduction avec un tableau de proportionnalité :

Prix en €	59	100
Réduction en €	17,7	30
	Situation du problème	Pourcentage

- Appliquer la réduction :
59-17,70=41,30

En une seule étape : tableau « avant / après »
30% c'est 30 pour un total de 100

Prix avant réductuion en €	59	100
Prix après réductuion en €	41,30	70
	Situation du problème	Pourcentage

IV - Vitesses

La vitesse (moyenne) V d'un objet parcourant la distance d en un temps t est .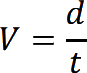

Un camion roule à 90km/h.
1 - Quel temps lui faut-il pour parcourir 150km ?
2 - Quelle distance parcourt-il en 1h20 ?

On utilise toujours la plus petite unité de temps qui apparait dans le problème pour éviter les écritures décimales du temps.

1h20 = 80min mais 1h20≠1,20h