Activité : Lecture de graphiques
Exemple : La part du lion
Les deux graphiqes circulaires ci-dessous représentent la part des aides sociales (partie A en vert) dans la dépense publique pour deux villes.
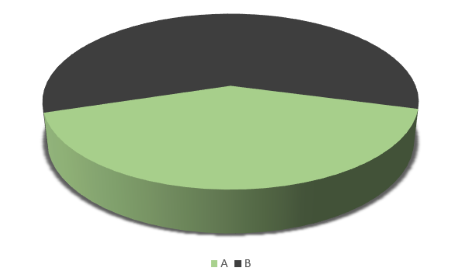
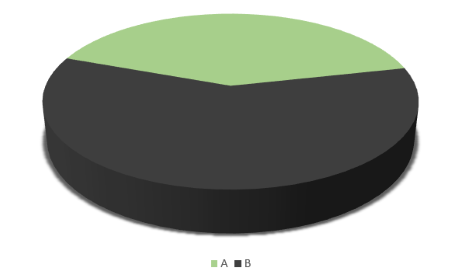
Dans la première, ces dépenses se taillent la part du lion, alors que dans la seconde, elles sont plus modérées.
Cette affirmation est-elle vraie ?
Cliquez pour voir la solution
Les diagrammes 3D sont peut-être élégants, mais leur perspective peut fausser notre perception. Les deux graphiques illustrent en fait la même réalité.
Exemple : La fin du mariage
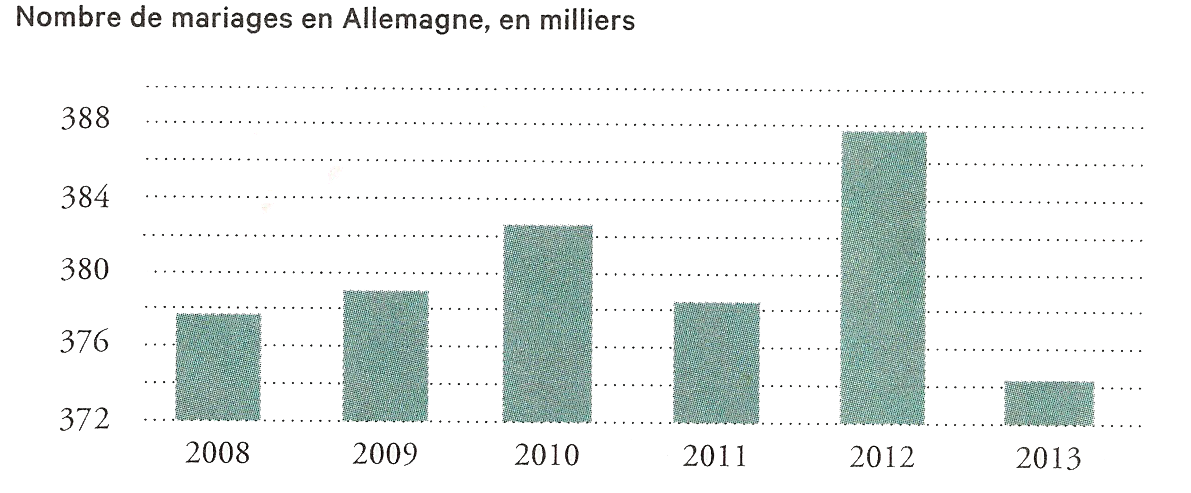
Le nombre de mariage s'effondre en Allemagne.
Cette affirmation est-elle vraie ?
Cliquez pour voir la solution
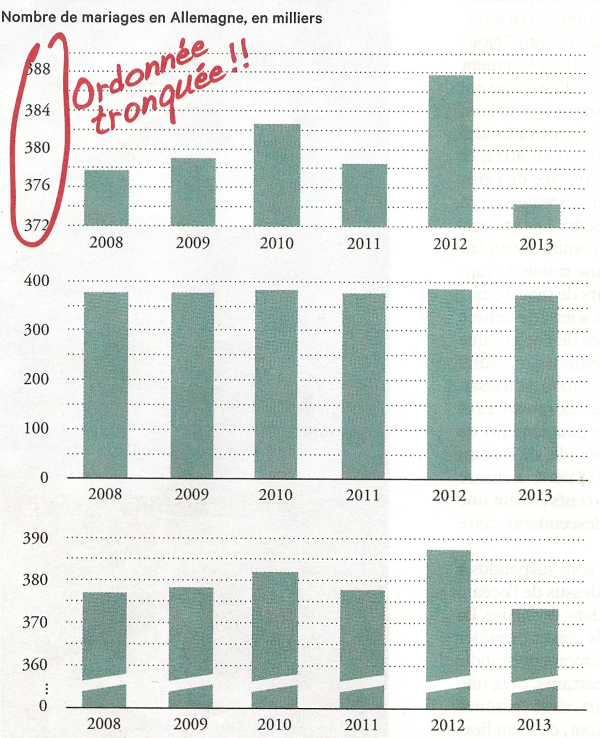
En zoomant sur une portion de l'ordonnée et en ne la faisant pas commencer à zéro, un graphique peut exagérer des écarts et des variations (premier graphique).
En réalité, on constate que le nombre de mariage évolue peu (deuxième graphique).
Pour représenter correctement ces variations, il faut raccourcir l'ordonnée et les colonnes de manière visible et égale (troisième graphique).
Exemple : L'euro, ça monte ou ça descend ?
Le graphique ci-dessous représente le cours de l'euro en dollars. Par exemple, le 13 mars 2015, 1€ valait un peu plus de 1,04$.
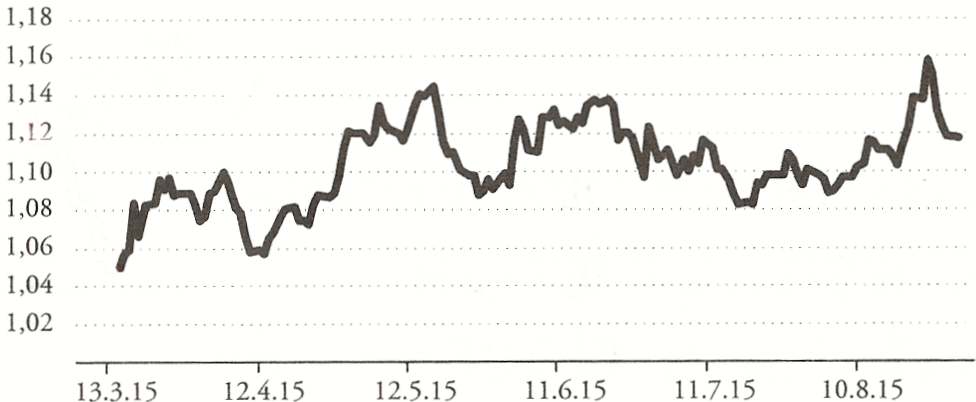
L'euro monte face au dollar.
Cette affirmation est-elle vraie ?
Cliquez pour voir la solution
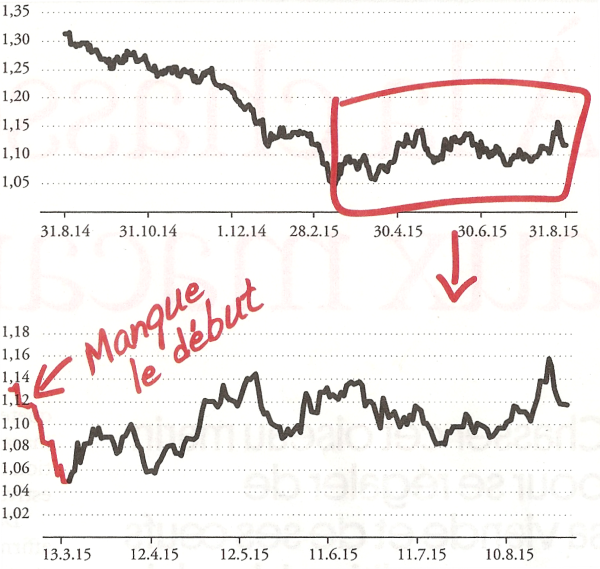
Les cours des actions boursières sont toujours représentés sur un axe d'ordonnée tronqué afin de faire apparaitre d'infimes variations de valeur.
Il est toutefois possible, en choisissant le début et/ou la fin de la période observéé, de faire croire à une tendance plutôt à la hausse ou plutôt à la baisse.
Exemple : Les dépenses militaires de l'Allemagne
Les dessins ci-dessous représentent les dépenses militaires de l'Allemagne, en milliards d'euros :

Entre 1991 et 2014, les dépenses militaires de l'Allemagnes ont baissé.
Cette affirmation est-elle vraie ?
Cliquez pour voir la solution
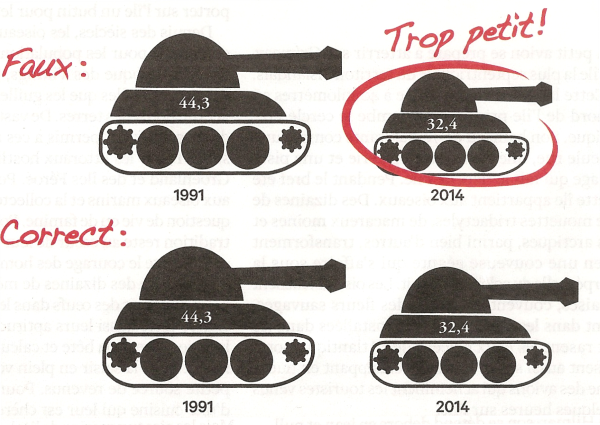
Une erreur classique consiste à utiliser un objet pour représenter des grandeurs mais sans respecter les règles de proportions.
Si on double la hauteur et la largeur, on a en réalité quadruplé la valeur représentée.
Le cas échéant, on accentue les écarts (premier graphique) alrs que ceux-ci ne sont pas si élevés (second graphique).
Dans le cas des objets tridimensionnels, un doublement des dimensions équivaut à multiplier le volume par 8.
Source : Courrier Internationnal n°1394







