D2 - Statistiques

Lors d'une étude statistique, on étudie sur une population un caractère qui peut prendre plusieurs valeurs.

On a interrogé 20 élèves de 5ème sur leur sport préféré. Voici leurs réponses :
F - B - D - H - F - D - B - H - F - F - B - T - D - D - F - B - F - T - F - B
Légende : F : Football - B : Basket - D : Danse - H : Handball - T : Tennis

Dans cette enquête, la population étudiée est celle des élèves d'une classe.
Le caractère étudié est le sport préféré des élèves.
Les valeurs possibles du caractère sont : Football, Basket, Danse, Handball et Tennis.

II – Fréquence – pourcentage

La fréquence d'une valeur est le quotient :
Effectif de la valeur
Effectif total

Elle peut être exprimée sous forme décimale (exacte ou approchée) ou fractionnaire.
C'est un nombre entre 0 et 1.
Plus la fréquence est grande, plus la valeur est fréquente…

La somme des fréquences doit être égale à 1

La fréquence en pourcentage est l'écriture de la fréquence sous forme de pourcentage :
Effectif de la valeur
Effectif total
× 100 La somme des fréquences en pourcentage doit être égale à 100%

Avec les données précédentes
Sport F B D H T Total
Effectif 7 5 4 2 2 20
Fréquence
7
20
5
20
4
20
2
20
2
20
20
20
= 1
Fréquence en % 35% 25% 20% 10% 10% 100%

III – Représentations graphiques

1 – Diagramme en barres

Dans un diagramme en barres, la hauteur de chaque barre est proportionnelle à l'effectif ou à la fréquence qu'elle représente

Avec les données précédentes
Sport F B D H T Total
Effectif 7 5 4 2 2 20

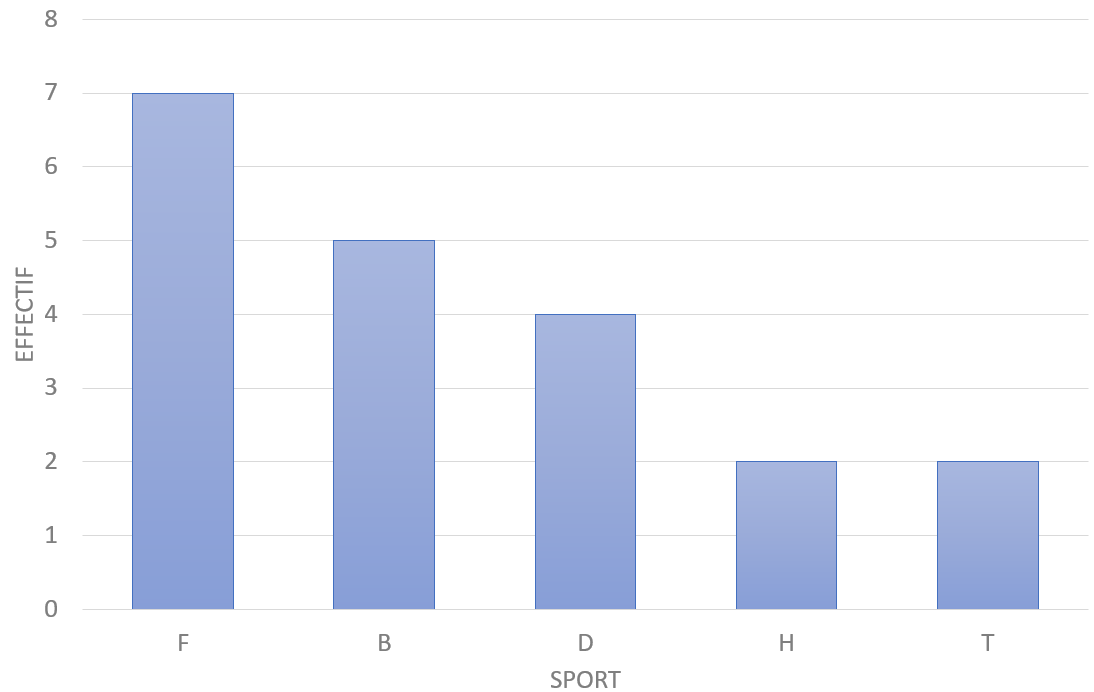
Il n'y a pas d'échelle sur l'axe horizontale mais le nom de chaque barre (ce qu'elle représente).

2 – Diagramme circulaire

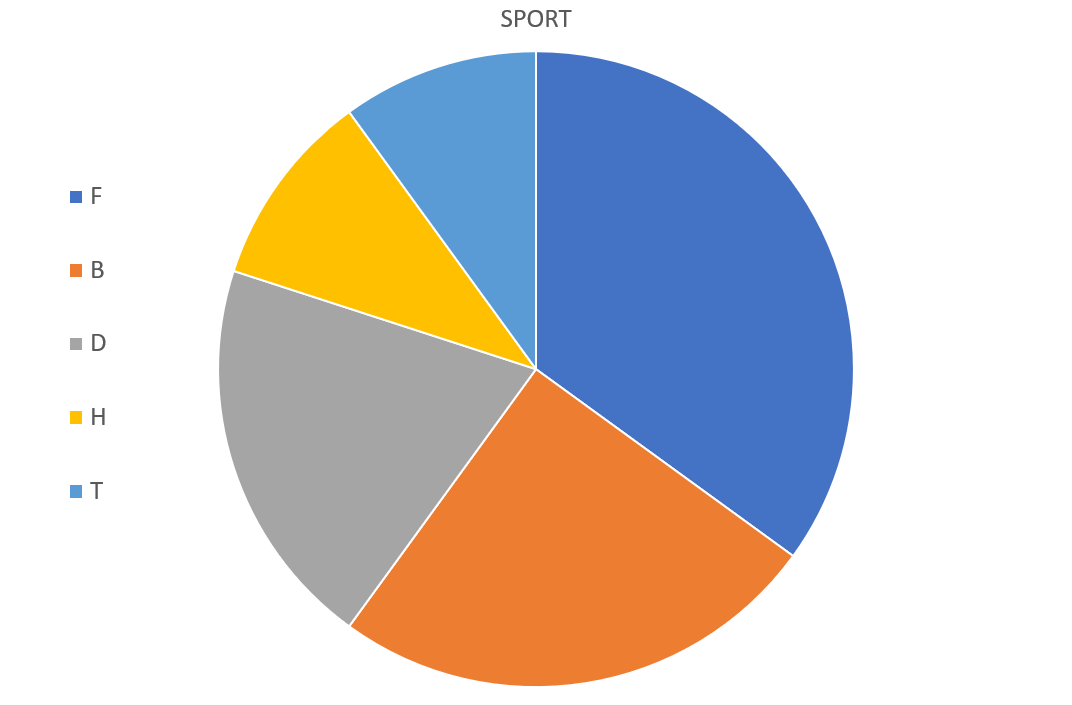
Dans un diagramme circulaire, l'angle de chaque secteur est proportionnelle à l'effectif ou à la fréquence qu'elle représente

Avec les données précédentes
Sport F B D H T Total
Effectif 7 5 4 2 2 20
Angle en ° 126 90 72 36 36 360

IV – Moyenne d'une série

Dans la suite de ce cours, on va utiliser les données suivantes qui sont des rélevés de notes de trois élèves.
Voici les dernières notes qu’ont obtenues 3 élèves :
Jérôme : 4 ; 6 ; 18 ; 7 ; 17 ; 12 ; 12 ; 18
Bertrand : 13 ; 13 ; 12 ; 10 ; 12 ; 3 ; 14 ; 12 ; 14 ; 15
Yennefer : 15 ; 9 ; 14 ; 13 ; 10 ; 12 ; 12 ; 11 ; 10

Moyenne =
Somme des valeurs
Effectif total

MoyenneJérôme = (4 + 6 + 18 + 7 + 17 + 12 + 12 + 18) ÷ 8 = ......... ≈ ..........
MoyenneBertrand = (13+13+12+10+12+3+14+12+14+15) ÷ 10 = .......
MoyenneYennefer = (15 + 9 +14 + 13 + 10 + 12 + 12 + 11 + 10) ÷ 9 ≈ .......

La moyenne est une caractéristique de position.

On peut gagner du temps avec une moyenne pondérée ou moyenne avec coefficients.
Par exemple pour Bertrand il suffit de créer le tableau suivant :
Note 3 10 12 13 14 15 Total
Effectif 1 1 3 2 2 1 10
L’effectif de la note 12 est le nombre de fois qu’elle apparait dans la série des notes de Bertrand.
MoyenneBertrand = (1×3 + 1×10 + 3×12 + 2×13 + 2×14 + 1×15) ÷ 10

V – Médiane d'une série

La médiane est une valeur du caractère qui partage la population en deux parties de même effectif :
Ceux qui ont une valeur du caractère inférieure à la médiane
Ceux qui ont une valeur du caractère supérieure à la médiane


Pour déterminer les notes médianes, il faut ordonner les séries.
4 6 7 12 12 17 18 18 Combien de notes par sous-groupe ? 8÷2=4 donc 2 groupes de 4
On « fait » les groupes :
4 6 7 12 12 17 18 18 On détermine la médiane : un nombre entre le plus grand des plus petits et le plus petit des plus grands :
la médiane est 12.


Bertrand : 3 10 12 12 12 13 13 14 14 15.
10 valeurs donc deux groupes de 5. La médiane est entre la 5ème note (12) et la 6ème (13) : On choisit 12,5 pour médiane.

Yennefer : 9 10 10 11 12 12 13 14 15
9 valeurs donc deux groupes de 4 et il restera une note seule . 9 10 10 11 12 12 13 14 15 La médiane la valeur isolée : c’est 12

VI - Étendue d'une série

L’étendue d’une série statistique est la différence entre la plus grande valeur et la plus petite.

EtendueJérôme= 18-4 = 14
EtendueBertrand = 15-3 = 12
EtendueYennefer = 15-9 = 6