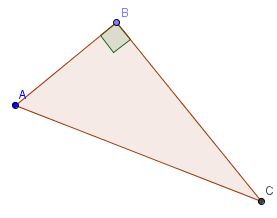
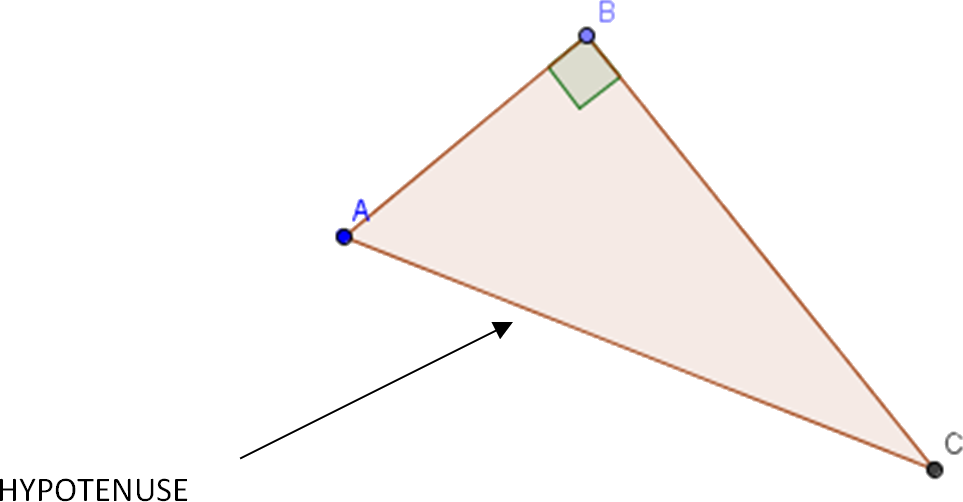
Le triangle ABC est rectangle en B. On a donc AC2 = BA2 + BC2
Propriété de Pythagore :
SI un triangle est rectangle
ALORS le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.

Le triangle ABC est rectangle en B. On a donc AC2 = BA2 + BC2
Ecrire l’égalité de Pythagore pour chacun des triangles rectangles suivants.
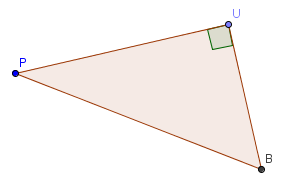
PB2 = PU2 + UB2
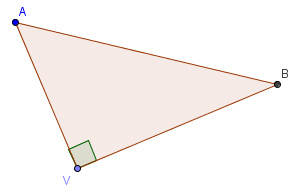
AB2 = VA2 + VB2
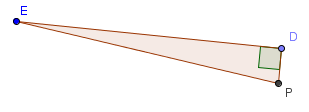
PE2 = ED2 + DP2
On utilise la propriété de Pythagore quand on a un triangle rectangle, qu’on connaît les longueurs de 2 côtés et qu’on veut calculer celle du troisième.
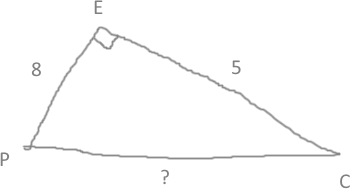
Soit PEC un triangle rectangle en E tel que EP=8cm et EC=5cm. Déterminer au millimètre près la longueur du côté [CP].
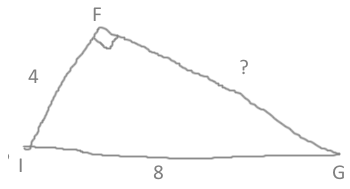
Soit FIG un triangle rectangle en F tel que FI=4cm et IG=8cm. Déterminer au millimètre près la longueur du côté [FG].