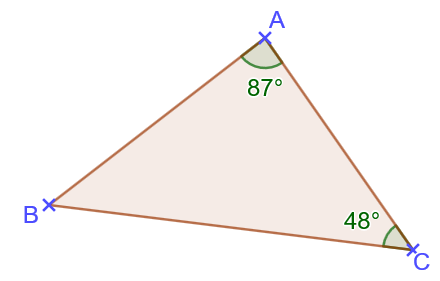
Calculer l'angle B.
A + B + C = 180°
B = 180 ° - (87° + 48°)
B = 45°
Dans un triangle, la somme des angles (aux sommets) est toujours égale à 180°

Calculer l'angle B.
A + B + C = 180°
B = 180 ° - (87° + 48°)
B = 45°
On dit que deux trianlges sont semblables quand ils ont les mêmes angles
Les triangles ABC et FDG sont semblables.
Il suffit de vérifier que deux couples d'angles sont égaux pour avoir des triangles semblables.
Quand deux triangles sont semblables, les longueurs de leurs côtés sont proportionnelles.
On dit que les triangles sont alors proportionnels.
Calculer des longueurs dans des triangles proportionnels.
Soit ABC et FDG les triangles proportionnels ci-dessous.
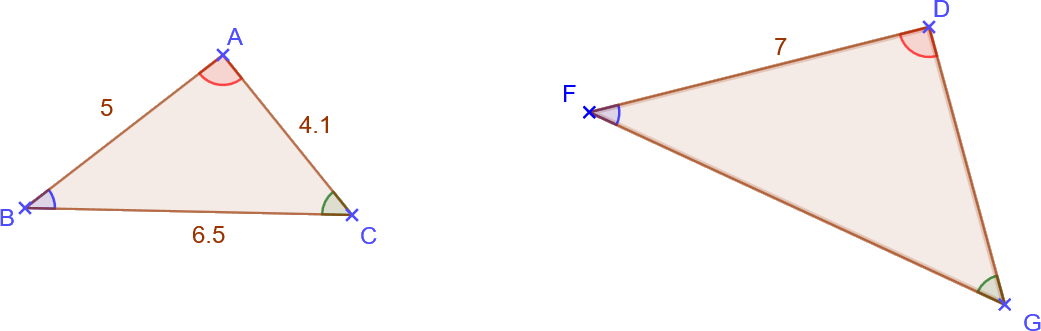
Calculer FG et DG.
Dresser le tableau de proportionnalité
| Triangle ABC | AC | CB | BA |
| Triangle FDG | DG | GF | FD |
| Triangle ABC | 4,1 | 6,5 | 5 |
| Triangle FDG | 7 |
| Triangle ABC | 4,1 | 6,5 | 5 |
| Triangle FDG | 5,74 | 9,1 | 7 |
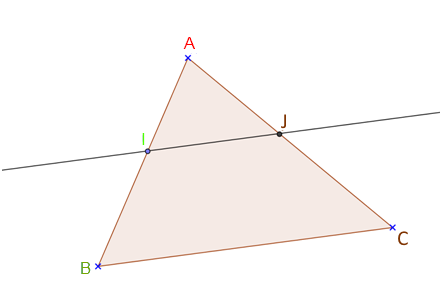
Dans un triangle ABC, I est un point du segment [AB] et J est un point du segment [AC].
SI (IJ) est parallèle à (BC)
ALORS les triangles AIJ et ABC sont proportionnels
| Triangle AIJ | AI | AJ | IJ | ||
| Triangle ABC | AB | AC | BC |
Si deux figures sont proportionnelles, on dit que l’une est l’agrandissement ou la réduction de l’autre.
Plus précisément avec des coefficients MULTIPLICATIFS :
| Triangle AIJ | 4 | 6 | 8 |
| Triangle ABC | 6 | 9 | 12 |
| 3 |
| 2 |
| 2 |
| 3 |
Dans un agrandissement/réduction, les angles, la perpendicularité et le parallélisme sont conservés.