G5 – Géométrie dans l'espace

0 – Activité

1 2 3 4

5 6 7 8

Voici quelques descriptions/définitions d'objets de l'espace:
tétraèdre:objet dont toutes les faces sont des triangles
prisme : objet ayant deux faces de bases polygonales parallèles et dont les faces latérales sont des parallélogrammes
tore : beignet
cylindre : tube
sphère : boule
Observe à l'écran les volumes ci-dessus et remplis le tableau suivant :

Figure	Numéro de l' (des)objet(s)
Prisme	1 2 3 4 5 6 7 8
Pyramide	1 2 3 4 5 6 7 8
Tétraèdre	1 2 3 4 5 6 7 8
Cône	1 2 3 4 5 6 7 8
Sphère	1 2 3 4 5 6 7 8
Cylindre	1 2 3 4 5 6 7 8
Cube	1 2 3 4 5 6 7 8
Tore	1 2 3 4 5 6 7 8

I – Pyramide

une pyramide est un solide qui a
une face de forme polygonale (avec plusieurs côtés) appelée base de la pyramide,
des faces latérales de forme triangulaire, ayant un sommet commun.

le sommet commun des faces latérales est le sommet de la pyramide

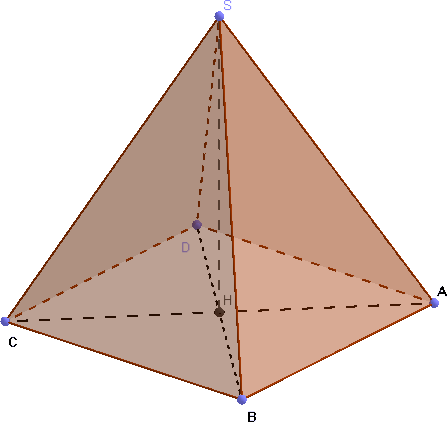Dans la pyramide SABCD,
le quadrilatère ABCD est la base.
les triangles SAB, SBC, SCD et SAD sont les faces latérales.
S est le sommet de la pyramide.
[SH] est la hauteur de la pyramide.
Patron d'une Pyramide :

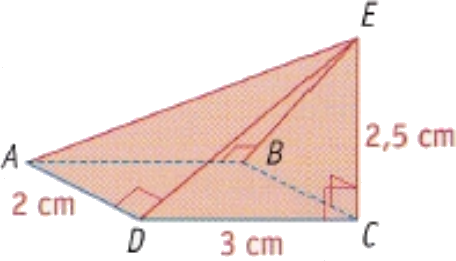La base est rectangulaire

l'aire latérale d'une pyramide est l'aire des faces latérales.

avec l'exemple précédent, l'aire latérale est égale à la somme des aires des 4 triangles rectangles du patron.

le volume V d'une pyramide est V =
1
3
× Aire de la base × hauteur.

II – cône de révolution

un cône de révolution est un solide obtenu en faisant tourner un triangle rectangle autour d'un des côtés de son angle droit.

Ce cône a été obtenu par rotaton du triangle rectangle SHA autour du côté [SH],
Le disque de centre H et de rayon HA est la base du cône.
S est le sommet de la pyramide.
[SH] est la hauteur du cône.
[SA] est une génératrice du cône.

le volume V d'un cône est V =
1
3
× Aire de la base × hauteur =
1
3
× π × r² × hauteur où r est le rayon de la base.