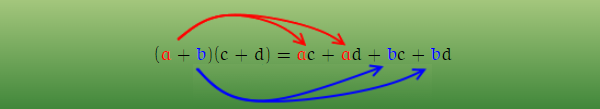
Pour tous nombres relatifs a, b, c et d :
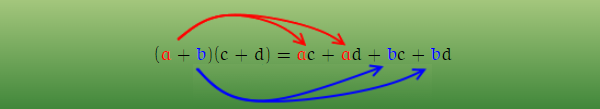
On peut traduire l'égaluité ci-dessus par une situation géométrique :
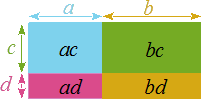 L'aire du grand rectangle est égale à la somme des aires des 4 petits.
L'aire du grand rectangle est égale à la somme des aires des 4 petits.
Développe et simplifie l'expression suivante : C=(3x+1)(2x+4)
On applique la double distributivité.
C=3x×2x+3x×4+1×2x+1×4
On effectue les produits et on simplifie.
C = 6x2+14x+4
Développe et simplifie l'expression suivante : D=(3x + 1)(y – 4).
On transforme la soustraction.
D=(3x + 1)(y +(-4))
On applique la double distributivité.
D=3x×y+3x×(-4)+1×y+1×(-4)
On calcule les produits et on simplifie.
D = 3xy–12x+y–4
on utilise deux fois la distributivité simple :
(a+b)(c+d)=(a+b)×c+(a+b)×d=a×c+b×c+a×d+b×d=ac+ad+bc+bd