 AB≤AC+BC
AB≤AC+BCAC≤AB+BC
BC≤AB+AC
On appelle triangle un polygone à 3 côtés (ou 3 angles)
 Les trois côtés du triangle ABC sont [AB], [AC] et [BC]. Ses trois sommets sont A, B et C. On peut aussi l’appeler ACB ou BAC ou CBA ou CAB ou BCA.
Les trois côtés du triangle ABC sont [AB], [AC] et [BC]. Ses trois sommets sont A, B et C. On peut aussi l’appeler ACB ou BAC ou CBA ou CAB ou BCA.
Un angle est dit plat quand il mesure 180°
Dans un triangle, la somme des angles doit être égale à 180°
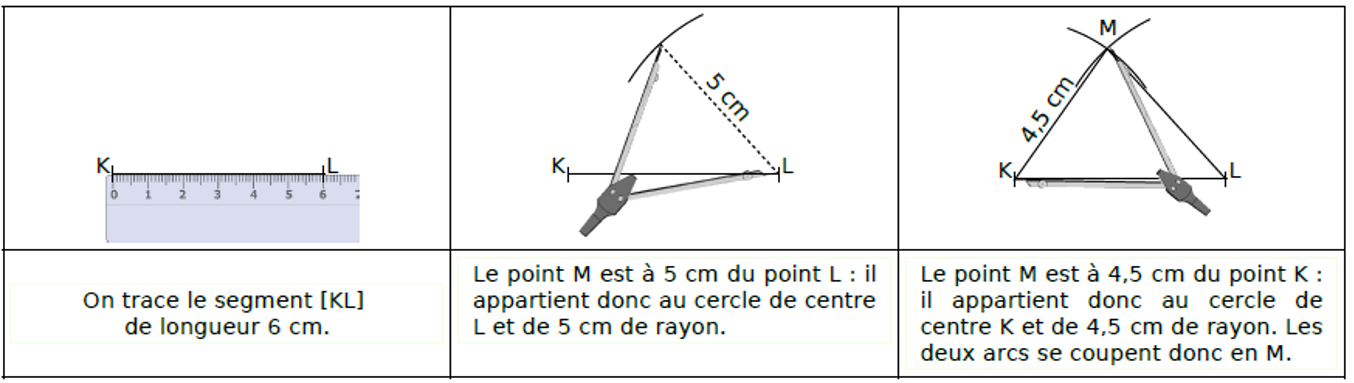
cliquez pour lire la videoDans un triangle, la longueur de chaque côté doit être inférieure à la somme des longueurs des deux autres.
Dans le triangle ABC on peut écrire 3 inégalités
 AB≤AC+BC
AB≤AC+BC
AC≤AB+BC
BC≤AB+AC
inégalité triangulaire.
Soit a, b et c trois nombres. On suppose que a est le plus grand des trois.
Si a≤b+c alors il existe un triangle dont les côtés mesurent a, b et c.
Si a≥b+c alors il n’existe pas de triangle dont les côtés mesurent a, b et c.
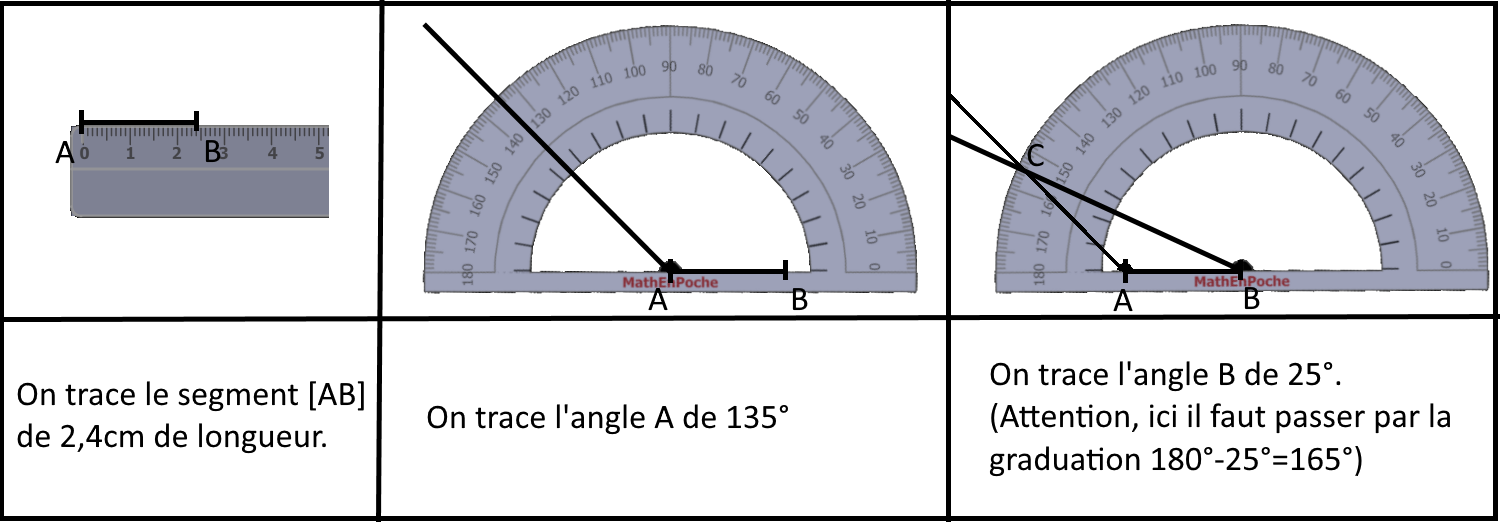
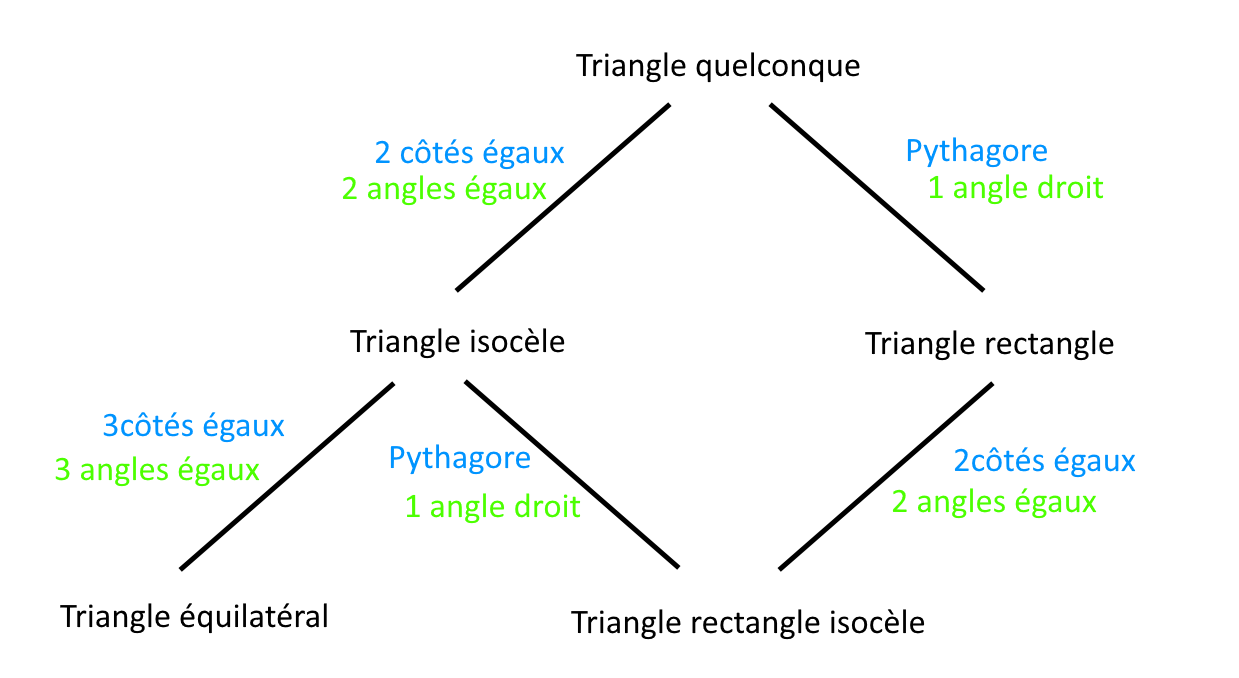
Un triangle est rectangle quand il a un (seul) angle droit.
Voir en quatrième la réciproque de Pythagore
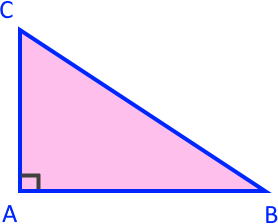 Le triangle ABC est rectangle en A.
Le triangle ABC est rectangle en A.
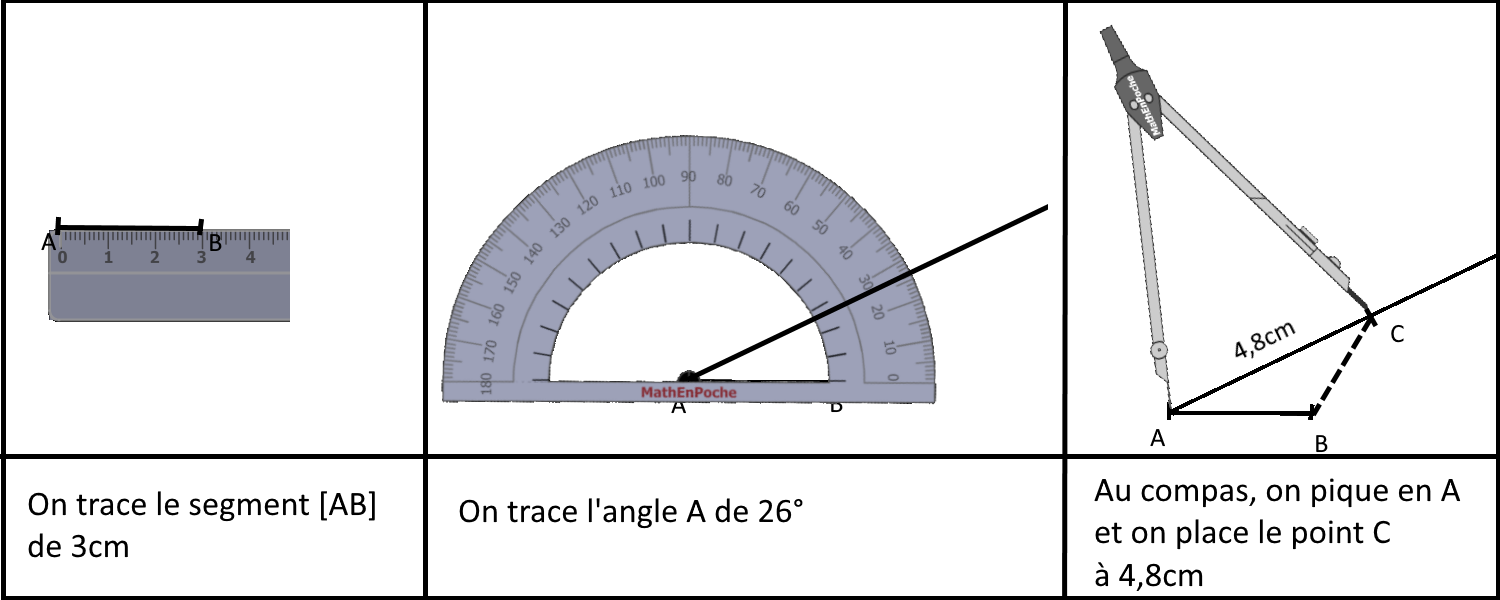
On utilise une équerre pour tracer un triangle rectangle.
Un triangle est isocèle quand il possède (au moins) deux côtés de la même longueur.
Un triangle est isocèle quand il possède (au moins) deux angles égaux.
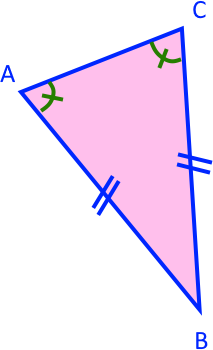 ABC est isocèle en B
ABC est isocèle en B
un triangle peut être à la fois rectangle et isocèle.
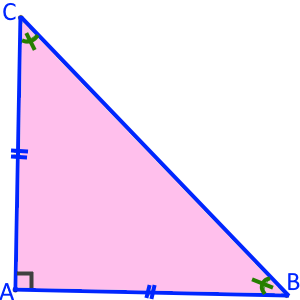 ABC est rectangle isocèle en A
ABC est rectangle isocèle en A
Un triangle est équilatéral quand ses trois côtés sont de la même longueur
Un triangle est équilatéral quand ses 3 angles sont égaux (à 60°)
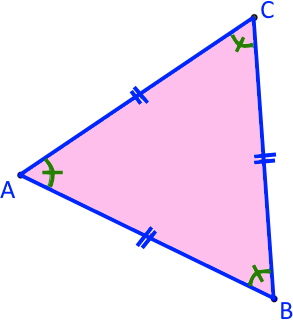 ABC est équilatéral.
ABC est équilatéral.