G2 – Symétrie centrale

I – Rappel : symétrie axiale

La symétrie axiale est définie par rapport à une droite, l'axe de symétrie.

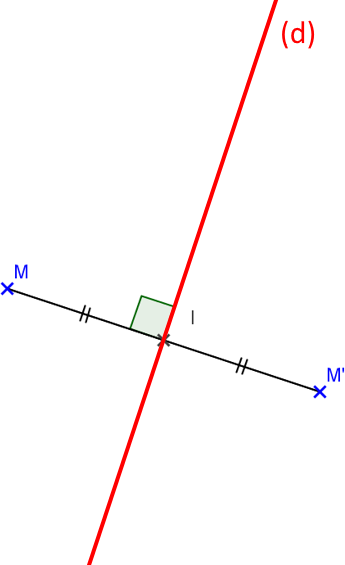
Soit (d) une droite et M un point qui ’appartient pas à (d).
Le symétrique du point M par rapport à (d) est le point M’ tel que la droite (d) soit la médiatrice du segment [MM’].

II – Symétrie Centrale

1 – Définition

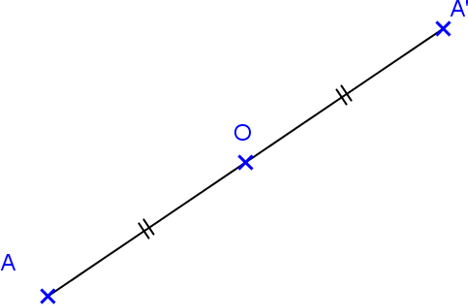
Deux points A et A’ sont symétriques par rapport à un point O quand O est le milieu du segment [AA’].

2 – Construction avec un quadillage

On suit le même chemin entre O et A’ qu’entre A et O en suivant les acrreaux.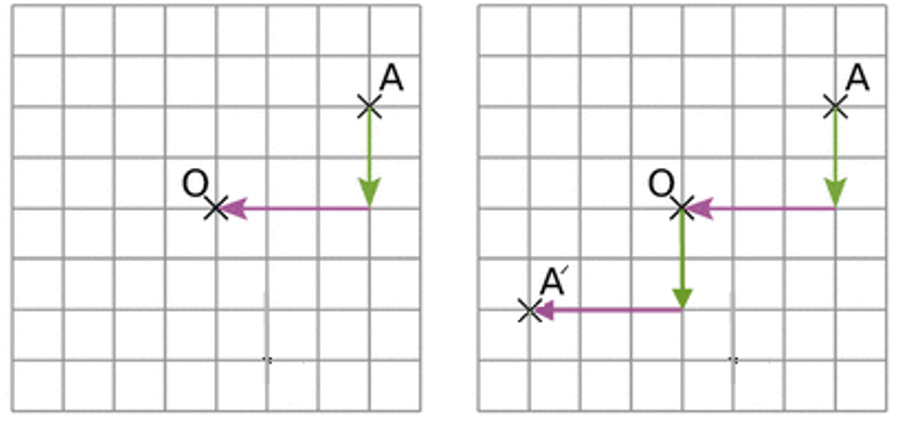

Attention à l’ordre des lettre dans la phrase ci-dessus : de A vers O puis vers A'

3 – Construction avec un compas

III – Constructions

1 – Symétrique d'un segment

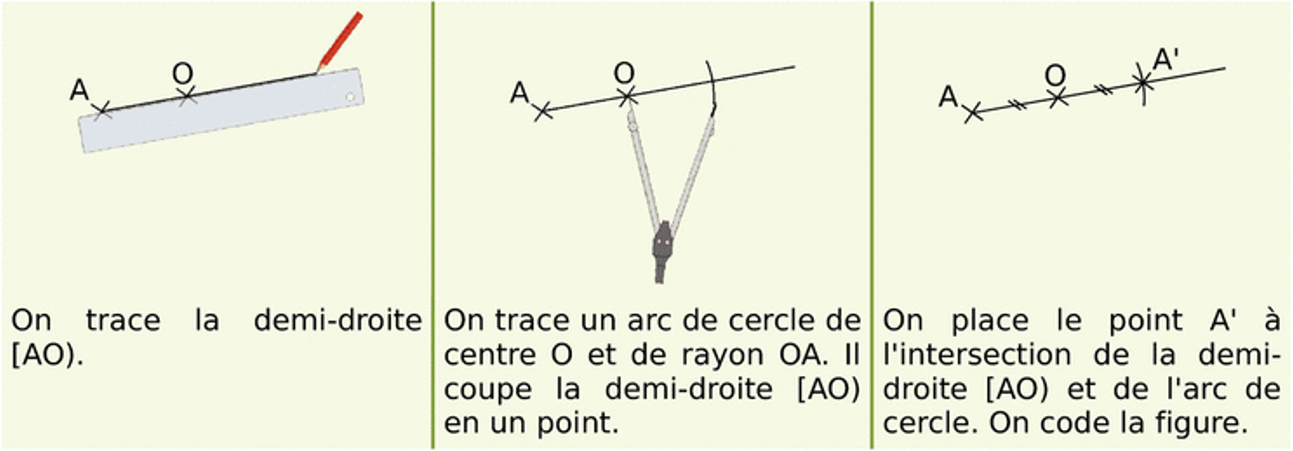
Pour construire le symétrique d'un segment, on construit les symétriques des deux extrémités du segment.

Cliquez sur l'image pour voir/cacher la solution

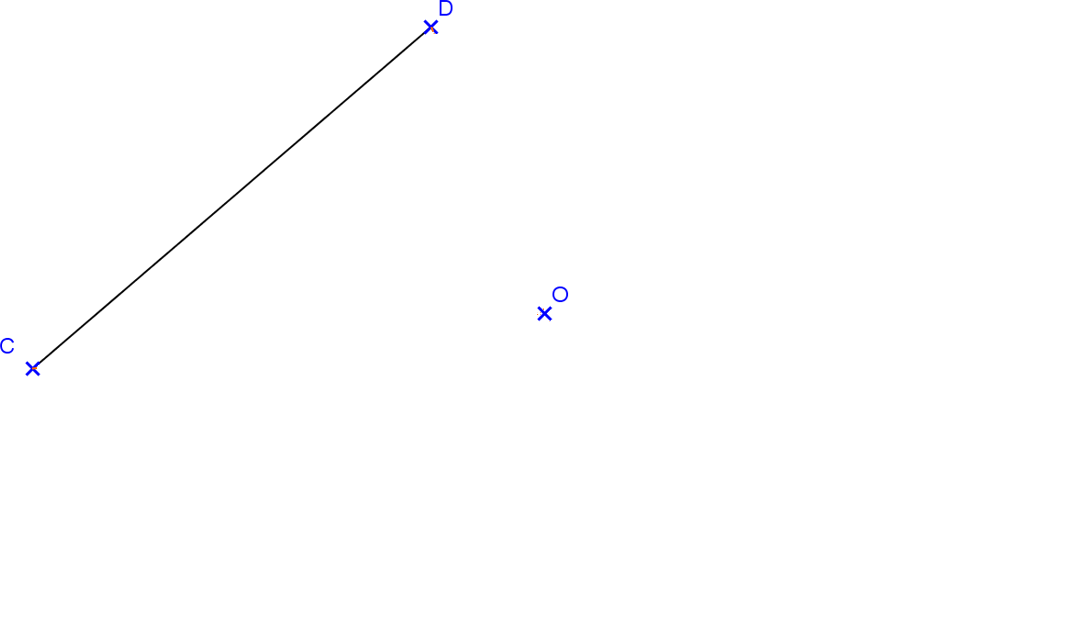
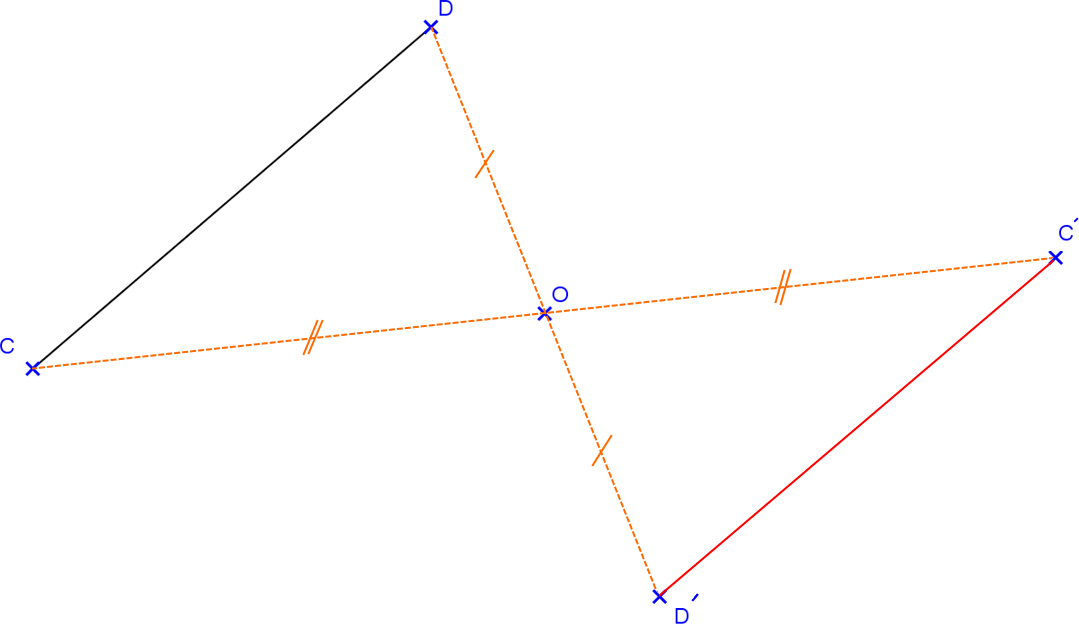
La droite symétrique d’une droite par rapport à un point est une droite parallèle.

2 – Symétrique d’un cercle

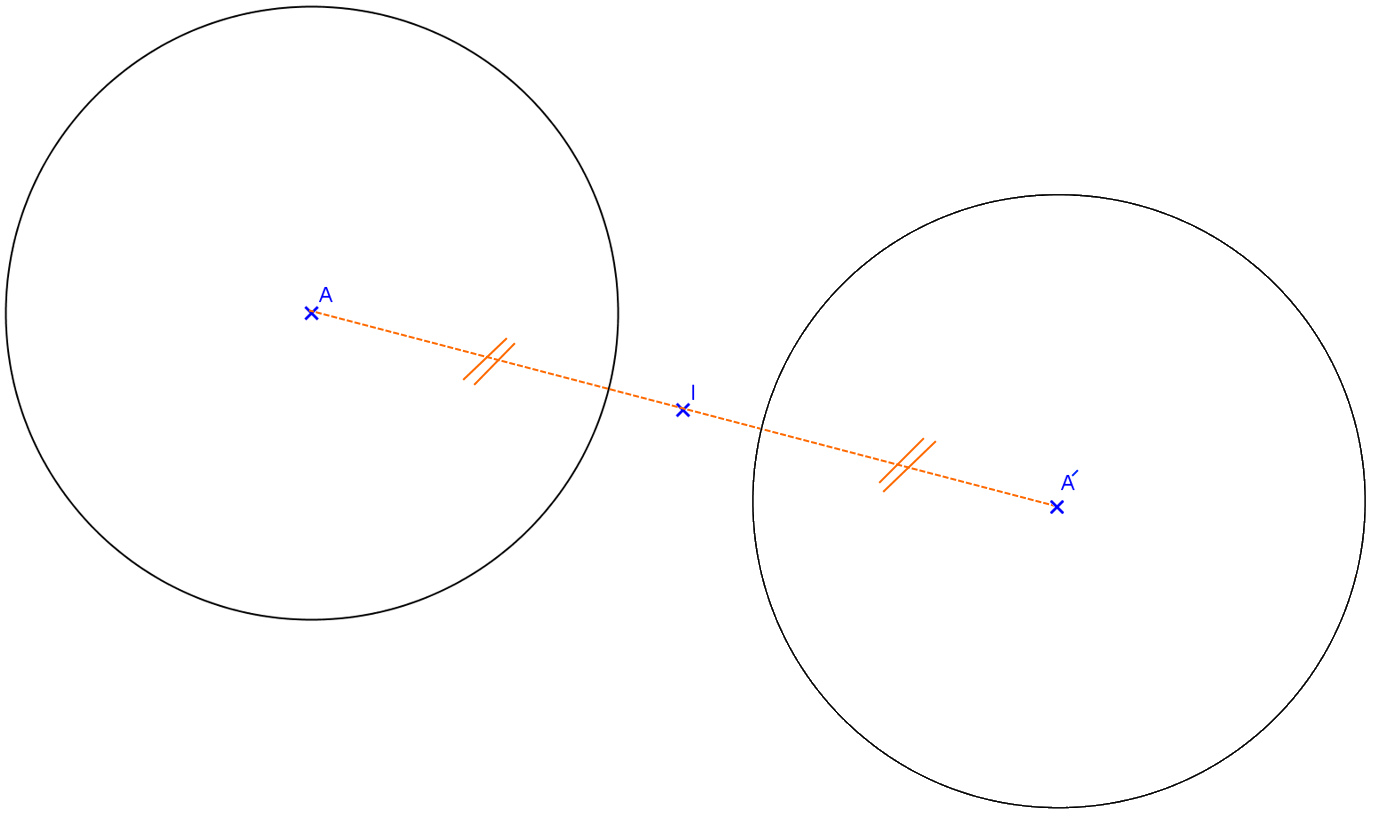
Le symétrique d’un cercle est un cercle de même rayon.

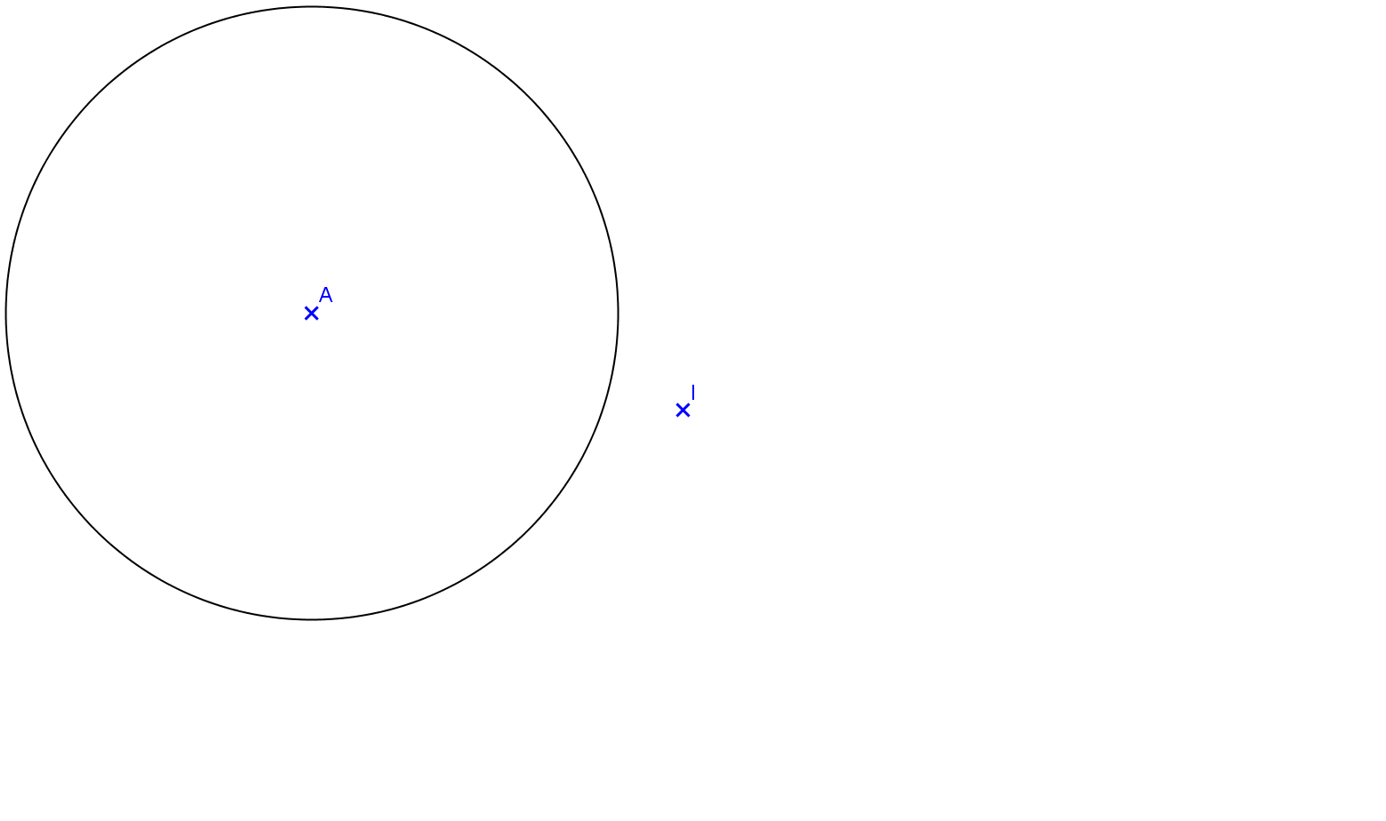
Pour construire le symétrique d'un cercle
Construire le symétrique A’ du centre A par rapport à I.
Tracer le cercle de centre A’ de même rayon que le cercle d’origine.

Cliquez sur l'image pour voir/cacher la solution

3 – Symétrique d’un triangle, d’un polygone

Le symétrique d’un polygone se construit segment par segment.

Cliquez sur l'image pour voir/cacher la solution

IV – Propriétés

La symétrie centrale conserve :
Les formes et les configurations
Les longueurs et les aires
Les angles
L'orientation

Différences avec la symétrie axiale :

Symétrie centrale

Symétrie axiale