| Nom | Figure codée | Définition |
| Médiatrice | La médiatrice d’un segment est la droite perpendiculaire qui passe par le milieu de ce segment. | |
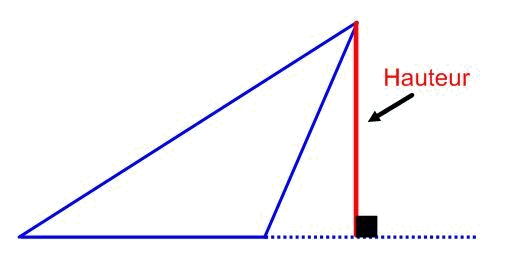
| Hauteur | La hauteur issue d’un sommet est la droite passant par ce sommet et perpendiculaire au côté opposé à ce sommet. | |
| Médiane | La médiane issue d’un sommet est la droite passant par ce sommet et par le milieu du côté opposé. | |
| Bissectrice | La bissectrice d’un angle est une demi-droite passant par le sommet et coupant l’angle en deux angles égaux. |
Dans un triangle
Les médiatrices sont concourantes
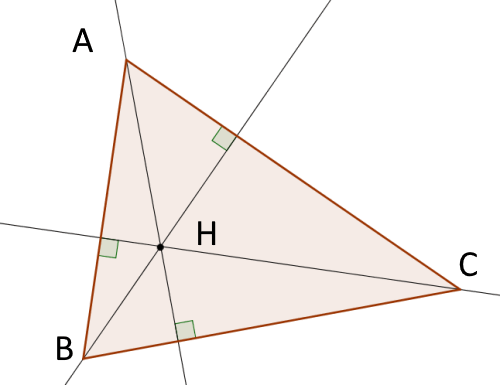
Les hauteurs sont concourantes
Les médianes sont concourantes
Les bissectrices sont concourantes
| Pour construire la médiatrice d'un segement [AB] | On trace deux arcs de cercle de centres A et B de même rayon (plus grand que la moitié de AB) | La médiatrice de [AB] est la droite qui passe par ces deux points. |
Soit [AB] un segment et (d) sa médiatrice.
Un point M situé sur la médiatrice (d) est à égale distance des extrémités A et B du segement.

Le cercle circonscrit à un triangle est le cercle qui passe par les 3 sommets du triangle.
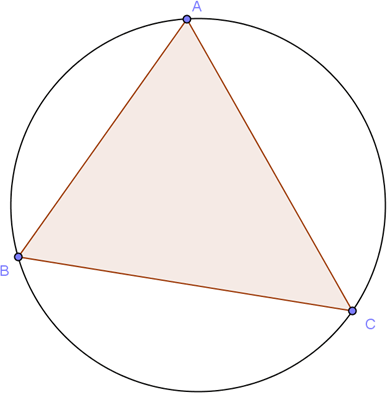
Le centre du cercle circonscrit à un triangle est l’intersection des médiatrices.
Preuve : Soit ABC un triangle et (ℂ) son cercle circonscrit. On appelle O le centre du cercle (ℂ).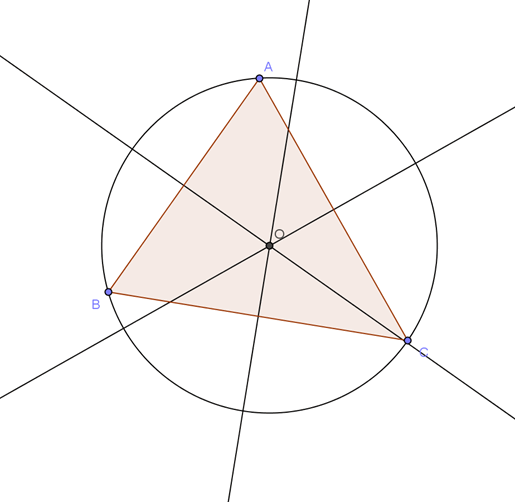
| Déposer un côté de l'angle droit de l'équerre sur la base du triangle. | Aligner l'autre côté de l'angle droit de l'équerre avec le sommet du triangle. | Tracer le segment qui part du sommet et qui rejoint perpendiculairement la base du triangle. Ce segment est la hauteur du triangle. |
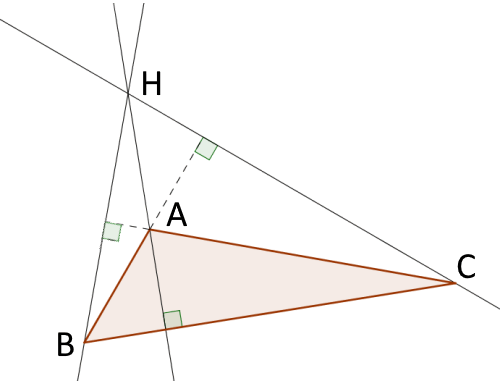
La hauteur d'un triangle peut parfois être à l'extérieur de celui-ci.
L'intersection des hauteurs d'un triangle est l'orthocentre de ce triangle
H est l'orthocentre du triangle ABC

