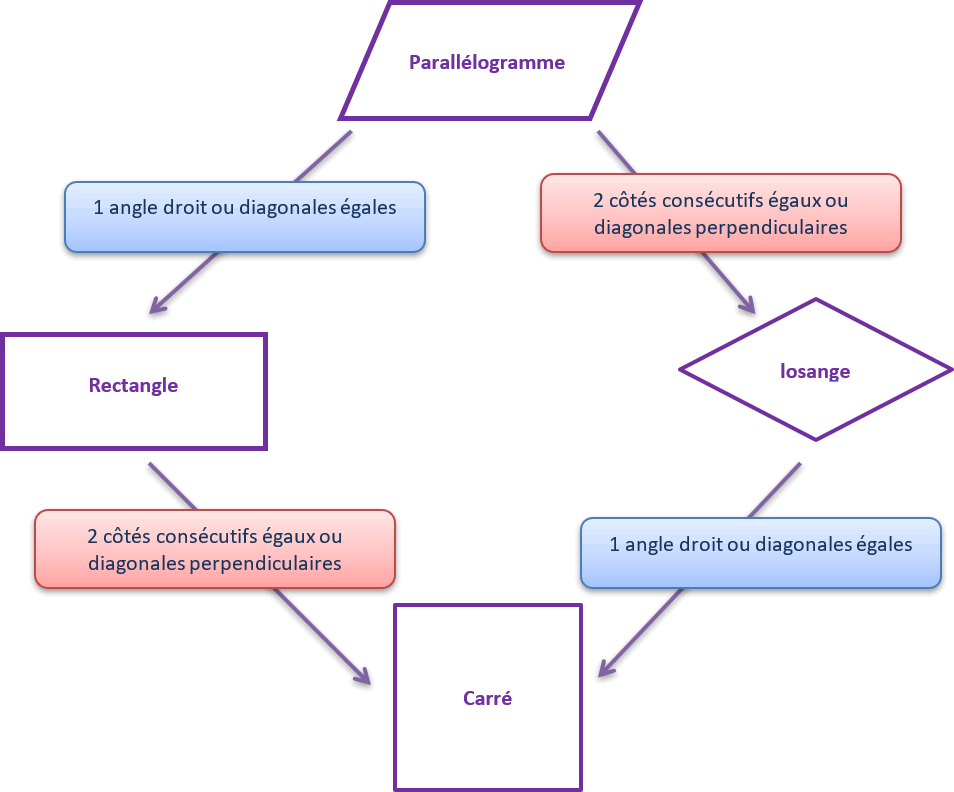
ses côtés opposés sont de la même longueur

ses diagonales se coupent en leur milieu
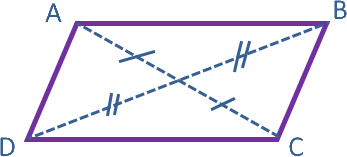
ses angles opposés ont la même mesure
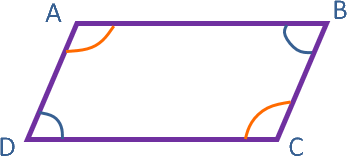
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.

Dans un quadrilatère, la somme des angles vaut toujours 360°
Si le quadrilatère ABCD est un parallélogramme, alors
ses côtés opposés sont de la même longueur
ses diagonales se coupent en leur milieu
ses angles opposés ont la même mesure
Chacune de ces propriétés peut être considérée comme une définition.
Par exemple, un parellélogramme est un quadrilatère dont les côtés opposés sont de la même longueur.
pour reconnaître un parallèlogramme, il suffit de vérifier qu'une paire de côtés sont de la même longueur ET parallèles.
Un rectangle est un quadrilatère qui a 4 angles droits.
Le rectangle est un quadrilatère qui a ses angles opposés de même mesure, alors le rectangle est un parallélogramme particulier.
Si le quadrilatère ABCD est un rectangle, alors
il a toutes les propriétés du parallélogramme.
ses diagonales ont la même longueur (et le même milieu).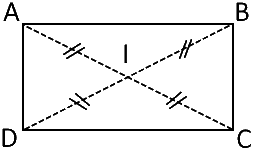
il a deux axes de symétrie (les médiatrices de ses côtés).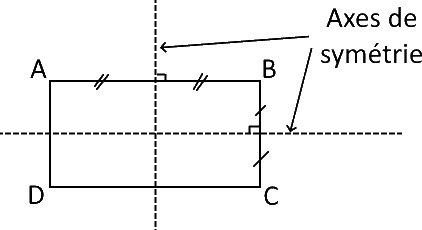
Reconnaitre un rectangle
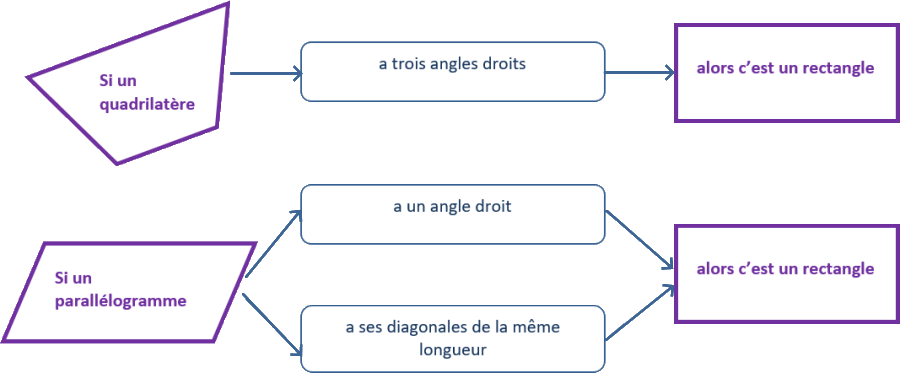
Un losange est un quadrilatère qui a 4 côtés de même longueur.
Le losange est un quadrilatère non croisé qui a ses côtés opposés de même longueur, alors le losange est un parallélogramme particulier.
Si le quadrilatère ABCD est un losange, alors
il a toutes les propriétés du parallélogramme.
ses diagonales sont perpendiculaires (et ont le même milieu).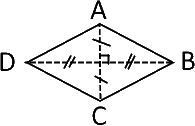
il a deux axes de symétrie (ses diagonales).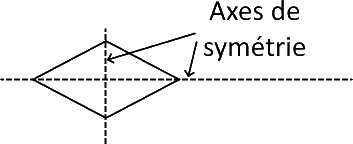
Reconnaitre un losange

Un carré est un quadrilatère qui a 4 angles droits et 4 côtés de même longueur.
Le carré est à la fois un rectangle et un losange, c'est un parallélogramme particulier.
Le carré a toutes les propriétés du parallélogramme, du rectangle et du losange
Pour reconnaître un carré, il faut reconnaître à la fois un rectangle et un losange.