N3 – Ecriture fractionnaire d'un nombre.

I – Fractions et quotient

La partie colorée représente
6
16
de la surface totale

Soit a et b deux nombres tels que b ≠ 0.
On note
a
b
le quotient de a par b.
On a alors :
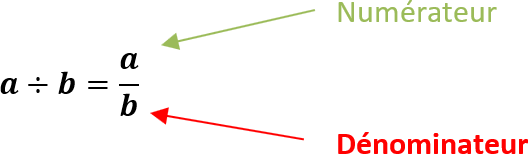
a ÷ b =
a
b

Vocabulaire :


2 ÷ 5 = \(2 \over 5\) = 0,4
3 ÷ 7 = \(3 \over 7\) ≈ 0,428571428571…

II – Fractions égales

1 – Égalité

On ne modifie pas la valeur d’une fraction lorsqu’on multiplie ou divise le numérateur ET le dénominateur par le même nombre non nul.
a
b
=
a × k
b × k
 ou
a
b
=
a ÷ k
b ÷ k


\({2 \over 3} = {{2×5} \over {3×5}} = {10 \over 15} \)

Complète
\({2 \over 5} = {6 \over …} = {… \over 45} \)
\({0,3 \over 1,2} = {… \over 0,4} = {0,6 \over …} \)

2 – Supprimer les nombres décimaux dans une fraction

Multiplier le numérateur et le dénominateur par 10, 100, 1000, etc…


\({1,08 \over 3} = {{1,08×100} \over {3×100}} = {108 \over 300} \)
\({1,084 \over 2,5} = {{1,084×1000} \over {2,5×1000}} = {1084 \over 2500} \)

3 – Simplifier une fraction

Simplifier une fraction c'est trouver une fraction égale écrite avec un numérateur et un dénominateur plus simple (c'est-à-dire plus petits)

On veut simplifier
25
15
.
On cherche une table de multiplication où 25 et 15 sont des résultats
25 = 5 × 5
15 = 3 × 5
On les rempace dans l'écriture de la fraction
25
15
=
5×5
5×3

On applique le théorème
25
15
=
5×5
5×3
=
5
3


27
45
=
3 × 9
5 × 9
=
3
5

On peut aussi écrire des divisions :
27
45
=
27 ÷ 9
45 ÷ 9
=
3
5

Une fraction qu'on ne peut plus simplifier est une fraction irréductible.

4 – Mettre deux fractions au même dénominateur

On veut réécrire les deux fractions
3
4
et
5
7
de telle sorte qu’elles aient le même dénominateur.
Comment trouver le dénominateur commun ?
Un dénominateur commun est un multiple commun à 4 et à 7 : c’est un résultat qui se trouve à la fois dans la table de multiplication du 4 et dans la table du 7.
Réponses possibles : 28 mais aussi 56, 84, etc…
\({3 \over 4} = {… \over 28} \)
\({5 \over 7} = {… \over 28} \)

mettre sur le même dénominateur
\({1 \over 4}\) et \({ 3 \over 10} \)
\({5 \over 8}\) et \({7 \over 12} \)

III – Comparaison de fractions

Si deux fractions ont le même dénominateur POSITIF, alors la fraction qui a la plus grand numérateur est la plus grande des deux fractions.


\({8 \over 15} < {9 \over 15} \)

Pour comparer des fractions, il faut :
Les mettre sur le même dénominateur POSITIF
Puis les ranger dans le même ordre que leur « nouveau » numérateur

Comparer \({5 \over 6}\) et \({7 \over 8} \) ?
On choisit un dénominateur commun : 6 × 4 = 8 × 3 = 24
\({5 \over 6} = {20 \over 24} \)
\({7 \over 8} = {21 \over 24} \)
Donc \({5 \over 6} < {7 \over 8} \)

Ranger par ordre décroissant \({3 \over 10}\), \({2 \over 5}\) et \({1 \over 20}\).