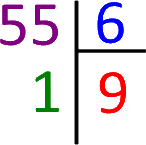55 = 6 × 9 + 1Soient a et b deux nombres entiers, avec b ≠ 0.
Effectuer la division euclidienne de a par b, c'est trouver deux nombres entiers uniques q et r tels que a = b × q + r avec r < b .
Vocabulaire :
Le nombre a est appelé dividende.
Le nombre b est appelé diviseur.
Le nombre q est appelé quotient.
Le nombre r est appelé reste.
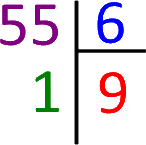55 = 6 × 9 + 1
Il est fondamental que le reste soit inférieur (strictement) au diviseur car sinon, ni le quotient, ni le reste ne sont uniques.
55 = 6 × 9 + 1 est la division euclidienne de 55 par 6
55 = 6 × 8 + 7 n'est pas la division euclidienne de 55 par 6
55 = 6 × 5 + 25 n'est pas une division euclidienne.
Premier prérequis : il faut connaître les tables de multiplication
Dans des cas simples : dividende inférieur et diviseur inférieur à 10 dans les tables de multiplication.
Par exemple si on veut diviser 62 par 8, on se pose la question « Dans 62 combien de fois 8 ? »
Il faut donc trouver le résultat de la table du 8 immédiatement inférieur à 62 : c'est 56 et c'est 8 × 7
« Dans 62 combien de fois 8 ? 7 fois »
Toujours dans des cas simples, une fois qu'on a déterminer le quotient on calcule le reste;
Par exemple dans la division de 62 par 8, on sait déjà que le quotient est 7 car 8 × 7 = 56.
Sur ses doigts, on compte : « 56 pour aller à 62, il faut 6 »
En conclusion : « Dans 62 combien de fois 8 ? 7 fois et il reste 6». Autrement écrit :
fois et il reste .
Diviser n'importe quel nombre par un nombre inférieur à 10
On veut diviser 127 par 8. On commence par poser l'opération :
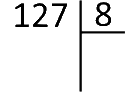La première chose à faire est de choisir un nombre de chiffres suffisant au dividende pour pouvoir diviser par 8. Ici on prendra 12.
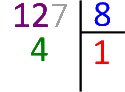« Dans 12 combien de fois 8 ? 1 fois et il reste 4 ». On abaisse le chiffre suivant au dividende : le 7.
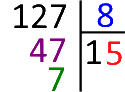« Dans 47 combien de fois 8 ? 5 fois et il reste 7 »
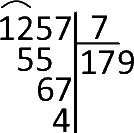
Division euclidienne :
On veut diviser 4534 par 58. On commence par poser l'opération :
« Dans 453 combien de fois 58 ? ».
On va remplacer cette question par une plus simple qui aura une réponse qui pourrait être la bonne :
« Dans 450 combien de fois 60 ? » qui deviendra en divisant les deux nombres par 10 (pour ne plus avoir de 0 au diviseur) :
« Dans 45 combien de fois 6 ? 7 fois ».
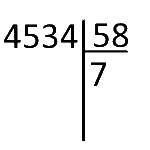Il faut maintenant calculer 58 × 7 puis soustraire ce produit de 453 pour calculer le reste.
Si le reste est inférieur à 58, on passe à l'étape suivante
Si le reste est supérieur à 58, il faut remplacer 7 pour 8, calculer 58 × 8, et calculer le nouveau reste puis passer à l'étape suivante.
Si 58 × 7 est supérieur à 453, on remplace 7 par 6 et on calcule le nouveau reste puis on passe à l'étape suivante.
Dans tous les cas, les opérations sont difficiles et/ou longue à faire.
Calcul rapide du reste :
On commence par multiplier le chiffre du quotient par le chiffre des unités du diviseur 7 × 8 = 56 qu'il faut soustraire du chiffre des unités du dividende.
« 56 pour aller à 3 » c'est impossible.
On remplace donc 3 par le premier nombre supérieur ou égal à 56 qui se termine par 3 : 63.
On écrit 6 en retenue et on compte sur ses doigts pour obtenir la répinse : « 56 pour aller à 63, il faut 7 »
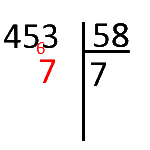
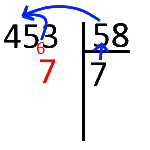
On recommence avec les chiffres des dizaines. 7 × 5 = 35, on ajoute la retenue 35 + 6 = 41 pour aller à 45 il est faut 4 (on prend 45 car il n'y aplus de chiffre à prendre au dividende).
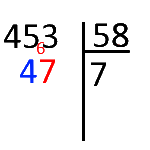La division est terminée. Le reste vaut 47.
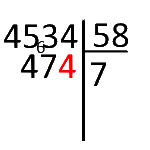
On abaisse le chiffre suivant (le 4) et on recommence comme au début : « Dans 474 combien de fois 58 ? »
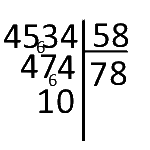
La division est terminée : « Dans 4534 combien de fois 58 ? 78 fois et il reste 10»
Soient a et b deux nombres entiers, avec b ≠ 0.
On dit que b est un diviseur de a quand le reste de la division euclidienne de a par b est égal à 0.
Cela revient à dire qu'on peut écrire a = b × k où k est un nombre entier.
4 est un diviseur de 32 car 32 = 4 × 8.
Un nombre a toujours au moins un diviseur : 1 est un diviseur de n'importe quel nombre.
Un nombre est toujours un diviseur de 0.
Un nombre est toujours son propre diviseur.
Soient a un nombre entier non nul.
Les diviseurs de a lui sont tous inférieurs ou égaux.
Les diviseurs de 12 sont 1 - 2 - 3 - 4 - 6 - 12
Critères de divisibilité
Un nombre est divisible par 2 quand il est pair, c'est-à-dire qu'il se termine par 0,2,4,6 ou 8.
Un nombre est divisible par 3 quand la somme de ses chiffres est divisible par 3 : 735 est divisible par 3 car 7+3+5 = 15.
Un nombre est divisible par 4 quand le nombre formé par ses 2 derniers chiffres est divisible par 4 : 712 est divisible par 4 car 12 l'est.
Un nombre est divisible par 5 quand il se termine par 0 ou 5.
Un nombre est divisible par 9 quand la somme de ses chiffres est divisible par 9 : 3735 est divisible par 9 car 3+7+3+5 = 18.
Un nombre est divisible par 10 quand il se termine par 0.
Un nombre qui n'a que 2 diviseurs (1 et lui même) est appelé un nombre premier.
17 est un nombre premier. 12 n'est pas un nombre premier.