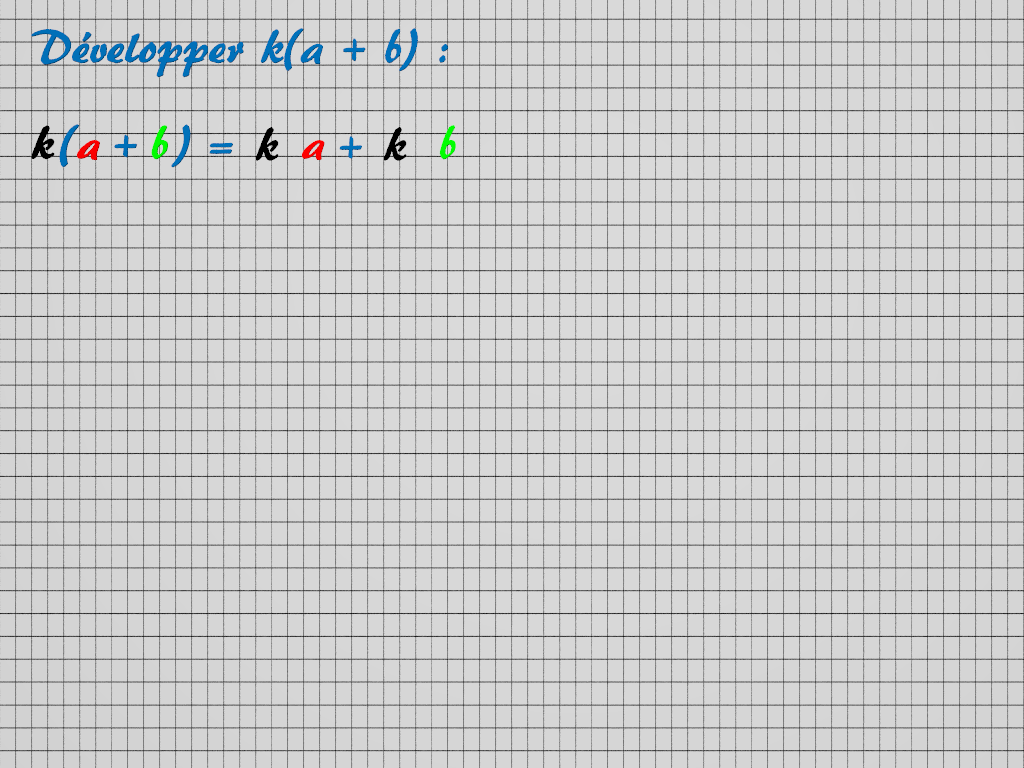
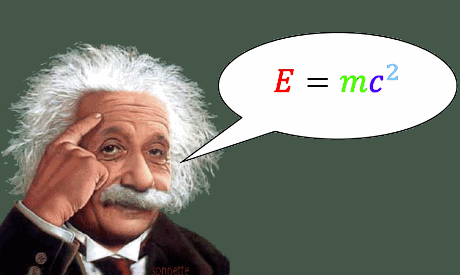
L’énergie E d’une particule est égale au produit de sa masse par le carré de la vitesse de la lumière.
Une expression littérale est une expression dans laquelle une ou plusieurs lettres désignent des nombres ou d’autres lettres.
L’aire d’un rectangle est donnée par la formule « Longueur fois largeur ».
Plus précisément, un rectangle de longueur L cm et de largeur l cm a une aire de L × l cm2.
Le prix d’un centre aéré est de 12 € à l’inscription et 2 € pour chaque journée. Le prix du séjour dépend du nombre de journées :
Le prix de 3 journées est donné par l’expression 12+2×3
Le prix de 6 journées est donné par l’expression 12+2×6
Le prix de x journées est donné par l’expression 12+2×x
Evaluer une expression littérale c’est remplacer chaque lettre par une valeur (donnée) et effectuer le calcul.
On rappelle que l’aire d’un disque de rayon r est donnée par la formule A=π×r×r.
Calculer l’aire pour r=4cm c’est évaluer l’expression A=π×r×r pour r=4 : A=π×4×4≈50cm2
On donne V=
. Calculer V pour d=12 et t=30.
d t
Une égalité comprend deux expressions appelées les membres et séparées par le signe « = ». Si les deux membres ont TOUJOURS la même valeur alors l’égalité est vraie.
L’égalité 15-3=10+2 est vraie car 15-3=12 et 10+2=12.
L’égalité 7×6=40+4 est fausse car 7×6=42 et 40+4=44.
Que dire de l’égalité 3 × x = x + 2 ?
Puisqu’on ne connait pas la valeur (numérique) de x, on ne peut rien dire pour l’instant.
Tester une égalité dont les membres sont des expressions littérales, c’est vérifier qu’elle est vraie quand on remplace les lettres par des nombres.
Pour x = 1, l’égalité 3 × x = x + 2 est vraie car 3 × 1 = 1 + 2.
Pour x = 5, l’égalité 3 × x = x + 2 est fausse car 3 × 5 ≠ 5 + 2.
On n’écrit pas le signe × sauf entre deux nombres.
3×x+2×6×x2=3x+2×6x2
5x+4=5×x+4
On écrit les nombres avant les lettres dans les multiplications « simplifiées ».
t×9=9t
8×(x×2+9)=8(2x+9)
On écrit les expressions avec des puissances quand c’est possible.
b×b=b2
r×r×r=r3
3×x×x=3×x2=3x2
l'addition est commutative. La multiplication est commutative.
2×x×6×x=2×6×x×x
a+b=b+a
l'addition est associative. La multiplication est associative.
2×3×x=2×(3×x)=(2×3)×x
2x×6x=(2×x)×(6×x)=2×x×6×x=2×6×x×x=(2×6)×(x×x)=12×x2=12x2
2+x+3+y=2+3+x+y=5+x+y
les priorités doivent être respectées
2+5×x=2+5x
(5x)3=5x×5x×5x
5x3=5×x×x×x
on peut remplacer n’importe quel caractère (lettre ou nombre) par n’importe quelle expression (lettre, nombre, expression)
x2=x×x
(5a)2=(5a)×(5a)
😜2=😜×😜
(
)2 = e-tiθ a2+b2
× e-tiθ a2+b2 e-tiθ a2+b2
2y+5y=7y
5x+3y=5x+3y
2×3x=6x
Réduire une somme c’est l’écrire avec le moins de terme possible en respectant les règles du calcul littéral.
3x+5x+9=8x+9
2a+5b+8a2+4b – 4a+a2=2a-4a+5b+4b+8a2+a2= – 2a+9b+9a2
On doit déplacer un terme avec le signe qui est DEVANT lui.
On ne peut pas déplacer des termes « prisonniers » dans des parenthèses
On veut réduire l’expression B=5x+8x2+(7x–4)–(1–3x2)
Pour supprimer des parenthèses dans une expression, il faut regarder ce qui précède les parenthèses :
Si les parenthèses sont précédées d’un signe +, alors on peut les supprimer sans rien changer
B=5x+8x2+7x–4–(1–3x2) Si les parenthèses sont précédées d’un signe –, alors :
On efface le signe – devant la parenthèse
On change tous les signes (+ ↔ –) à l’intérieur des parenthèses.
On supprime les parenthèses
Si des parenthèses sont précédées d’une multiplication, on peut développer pour « libérer » les termes des parenthèses.
Développer c’est transformer un produit en une somme ou une différence qui lui est égale.
Pour développer certaines expressions, on peut utiliser la distributivité simple.
Pour tous nombres k, a et b :
k(a + b) = ka+kb
k(a – b) = ka–kb
Développer puis réduire A=8(5x+4)
A=8(5x+4)
On applique la formule de distributivité
A=8×5x+8×4
On réduit chaque terme de l’addition
A=40x+32