1 axe de symétrie
2 axes de symétrie
Deux figures sont symétriques par rapport à une droite (d) si ces deux figures se superposent par pliage le long de cette droite.
Les figures 1 et 2 sont symétriques par rapport à la droite (d).
On dit aussi que la figure 2 est la symétrique de la figure 1 par rapport à l’axe (d).
Le point A est le symétrique du point M.
La droite (d) est appelée l’axe de symétrie.
Une droite est un axe de symétrie d’une figure F si la figure symétrique de F par rapport à la droite est la figure F elle-même.
Le symétrique d’un point M par rapport à une droite (d) est le point M’ tel que la droite (d) est la médiatrice du segment [MM’].
(d) est la médiatrice du segment [MM’]
M' est le symétrique de M par rapport à (d).
Puisque B est sur l’axe (d), il est son propre symétrique.
 |  |  |
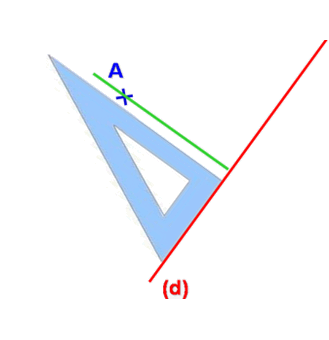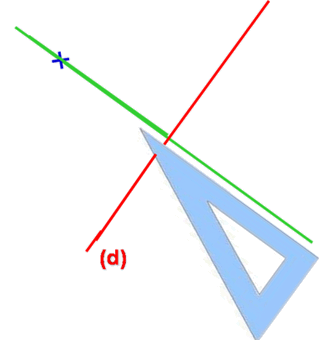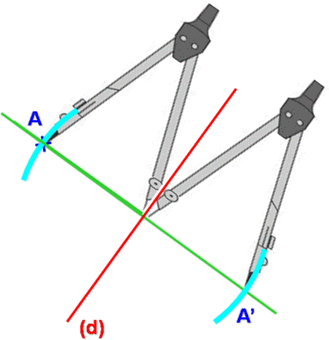| Avec l’équerre, on trace la perpendiculaire à la droite (d) passant par A. | Puis on prolonge le trait avec l’équerre. | Avec le compas on reporte la distance entre le point A et la droite (d)de l’autre côté de la droite. |
La symétrie axiale conserve les longueurs.
Le symétrique d’un segment est un segment de la même longueur.
A’ est le symétrique de A par rapport à (d).
B’ est le symétrique de B par rapport à (d).
[A’B’] est le symétrique du segment [AB] par rapport à (d).
On a A'B' = AB.
Le symétrique d’un cercle est un cercle de même rayon.
Plus précisément, si on appelle (C') le symétrique du cercle (C), le centre de (C') est le symétrique du centre du cercle (C).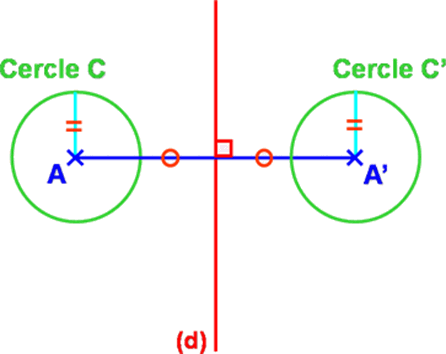
La symétrie axiale conserve l’alignement.
La symétrique d’une droite est une droite.
Il y a trois cas possibles :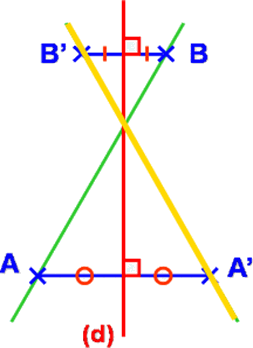
La droite (AB) est sécante avec l’axe : la droite symétrique (A'B') est concourante avec (d) et (AB)
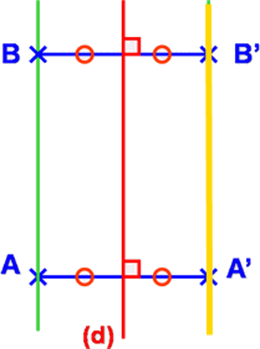La droite (AB) est parallèle à l’axe : la droite symétrique (A'B') est aussi parallèle à (d) et (AB)
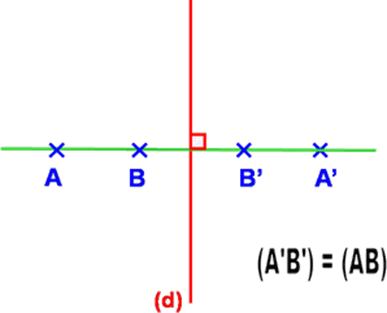La droite (AB) est perpendiculaire à l’axe : la droite (AB) est sa propre symétrique.
La symétrie axiale conserve les configurations.
Pour construire le symétrique d’une figure, on construit les symétriques de plusieurs de ses points et on utilise les propriétés de conservation.
La médiatrice d’un segment est un axe de symétrie de ce segment.
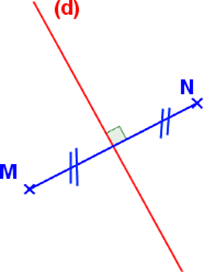
SI un point est sur la médiatrice d’un segment, ALORS il est équidistant des extrémités du segment.
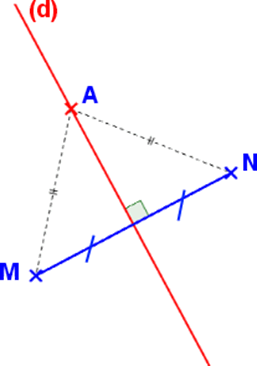A est sur la médiatrice de [MN] DONC MA=NA
SI un point est équidistant des extrémités d’un segment, ALORS il est sur la médiatrice de ce segment.
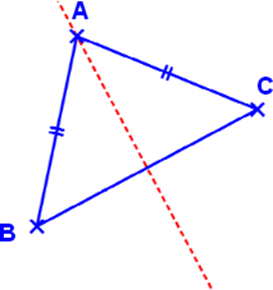MA=NA DONC A est sur la médiatrice de [MN]